In questo articolo approfondiamo alcuni concetti riguardanti i sensori digitali, in particolare i sCMOS (scientific CMOS). Quindi, daremo per assodate alcune definizioni come efficienza quantica, ADC, rapporto S/N, eccetera, con un’unica eccezione per il gain, sul quale faremo alcuni chiarimenti.
Il lettore che non vuole confrontarsi con la matematica necessaria al discorso troverà in fondo una ricapitolazione di quanto presentato.
1. Gain utente e gain di sistema
In generale, il gain (di qualunque tipo) esprime la conversione tra il segnale in elettroni (prima dell’ADC) ed il livello di luminosità in ADU. Si può scrivere:
E’ opportuno adesso distinguere tra gain utente gu e gain di sistema G. Il gain utente è quello settabile dal panello di controllo della camera, ed associato al concetto stesso di gain dalla maggior parte degli astrofili. In realtà esiste anche un’altro gain, definito dal produttore e sul quale non è possibile intervenire, definito gain di sistema. Il principio è quello di distribuire tutti i bit disponibili dopo la conversione operata dall’ADC sulla Full Well Capacity del sensore.
Facciamo un esempio, che tornerà utile anche in seguito. Supponiamo di avere un sensore con FWC 32.000 elettroni, ed un ADC a 12 bit (che dà quindi 2^12=4096 livelli di grigio). Il gain di sistema per questo sensore sarà dunque 32.000/4096=7,8 e-/ADU, e sono necessari quasi 8 elettroni per incrementare di una unità il conteggio degli ADU. In questo modo, a 32.000 elettroni sul fotosito, corrispondono esattamente 4096 ADU, ed abbiamo usato tutto il range dinamico del sensore. Questo gain è quello massimo in cui è possibile operare.
In realtà in astronomia si lavora in condizioni di luce scarsa, e si è quasi sempre affamati di fotoni, per cui è necessario agire su un altro parametro che prende appunto il nome di gain utente. Anche se di fatto amplifica il segnale a schermo, questo secondo tipo di gain va a dividere il gain di sistema, e per tale motivo si chiama anche gain inverso. Nel caso precedente, suppondendo un gain utente di 10x, avremo un gain effettivo di 0,78 e-/ADU, e quindi ci sarà bisogno di molto meno segnale (<1 elettrone, ossia 10 volte in meno di prima) per avere l’incremento di una unità di ADU. Abbiamo così ritrovato il concetto di gain come è inteso classicamente.
L’equazione precedente si scrive dunque più correttamente (si noti la posizione di gu, al denominatore):
o meglio (perché il segnale viene poi convertito):
Non è quindi il solo gain utente gu, ma il rapporto tra gain di sistema e gain utente G/gu a dare la reale conversione tra il segnale in e- nel fotosito e gli ADU; a parità di gu (gain utente) a una camera con una Full Well Capacity maggiore corrisponde un segnale maggiore (per gli stessi ADU), e inversamente, alla stessa FWC corrisponde un valore ADU maggiore a gain maggiore, com’è anche intuitivo. Si noti che mentre le unità di misura del gain di sistema sono quelle di e-/ADU, il gain utente è in effetti adimensionale, essendo un moltiplicatore.
Il gain utente si misura generalmente in decimi di decibel (0.1 dB). Il dB è definito a sua volta come:
quindi, in unità più comode (che sono quelle da inserire in pratica nel pannello di controllo della camera):
dove S2/S1 è il rapporto tra il segnale dopo e prima, ossia il altre parole il fattore di amplificazione.
Ogni 200 unità di gain utente il segnale (e il rumore) viene amplificato 10 volte, mentre ogni 60 raddoppia. Dall’equazione precedente segue che se gu=0 allora S2=S1. In questo caso, ovviamente, il segnale non viene amplificato, ed il gain che vediamo è quello di sistema. Casi simili capitano nella ripresa di oggetti molto luminosi, come il Sole o Venere in luce bianca. Il gain di sistema come visto all’inizio è pari a FWC/212, per un ADC a 12 bit.
Inversamente, supponendo di volere una amplificazione del segnale di 15 volte, possiamo scrivere
da cui si ricava gu=235.
Consideriamo un esempio pratico, relativo al sensore monocromatico IMX174MM. Il grafico seguente dà il gain totale (in ordinate) contro il gain utente. Il gain di sistema si legge dalla curva del gain al valore gu=0 ed è pari a circa 8 e-/ADU. Infatti, per questo sensore la FWC è pari a 32.000 e- e l’ADC è a 12 bit, quindi G=32.000/4096=7,8 e-/ADU (come già visto).
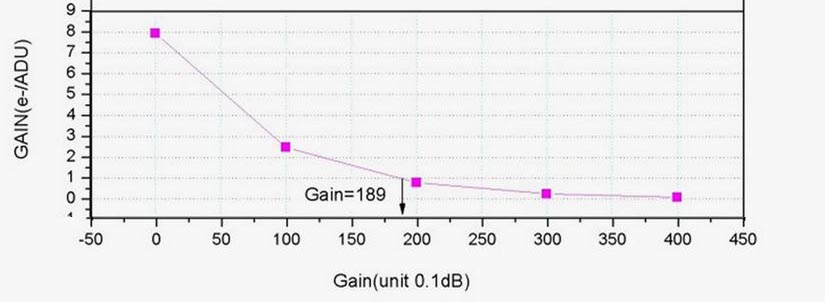
Ci si potrebbe chiedere cosa rappresenta su curve di questo tipo il valore di gain evidenziato (in questo caso 189). E’ il valore del gain unitario, ossia quello che ci permette di avere esattamente un gain di 1 e-/ADU. Settando quindi per la 174MM un gain di 189, avrò 100 ADU a schermo per un segnale nel well di 100 elettroni. Si calcola facilmente perché per definizione, l’amplificazione dev’essere pari a G ossia 7,8x, da cui
.
(il grafico sopra, probabilmente ricavato per punti, riporta un valore leggermente diverso).
Per fissare le idee prima di passare all’argomento successivo, supponiamo di avere un segnale N nel well di 25 elettroni (25 e-), e di amplificarlo di 10 volte (il sensore è sempre il 174MM). Come visto poc’anzi, a questa amplificazione corrisponde un gain utente di 200log(10)=200. Dopo l’ADC, che opera la conversione analogico-digitale, ho quindi naturalmente 25*10=250 elettroni (fittizi), a cui corrispondono ADU=(N*gu)/G=25*10/7,8=32 ADU, pari a sua volta a un istogramma del 32/4096=0,78% su 12 livelli di grigio.
Il rumore di fotoni associato sarà pari alla radice quadrata di 25 ossia 5 elettroni. Il rumore di lettura lo leggo dai grafici del produttore, come quello sottostante, al valore di gain selezionato (200): circa 3,8 elettroni.
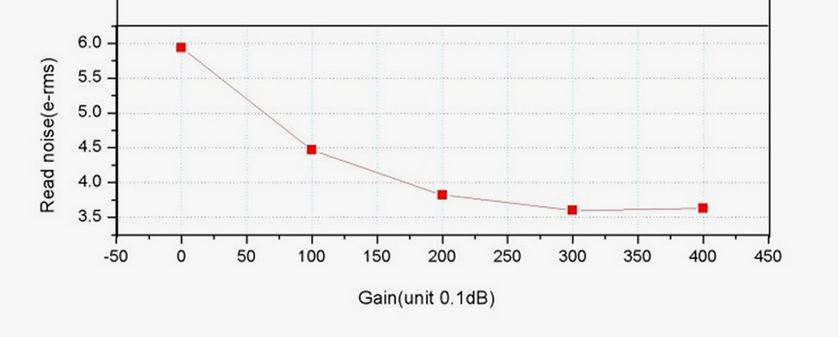
E’ importante distinguere qui tra il segnale prima dell’ADC (25 e-) e il segnale dopo l’ADC (32 ADU), e parimenti per il rumore (sia di lettura che di fotoni), che viene amplificato anch’esso dello stesso fattore 10.
2. Il rapporto segnale/rumore
Una misconception piuttosto comune tra gli astrofili è quella secondo cui aumentando il gain utente l’immagine a schermo diventi più rumorosa. Questa è in effetti l’impressione a prima vista, che però purtroppo è errata in quanto il rapporto segnale/rumore dell’immagine non cambia.
Il rapporto segnale/rumore è infatti definito come
dove N è il segnale (elettroni) e Np e Nr sono il photon noise (pari alla radice quadrata del segnale N) e il rumore di lettura (che non dipende dal segnale). In prima approssimazione, trascuriamo il rumore termico, che è ininfluente per gli oggetti luminosi con pose brevi, e notiamo che il termine prevalente del rumore è, nei casi ordinari, il rumore di fotoni.
Ad un qualunque gain utente, gu, il numeratore e il denominatore della relazione precedente sono moltiplicati per lo stesso fattore e quindi (trascurando la dipendenza di Nr da gu che lo fa diminuire leggermente) modificando il gain utente il rapporto S/N del singolo frame non cambia. Il rumore (essenzialmente di fotoni) diviene solo più evidente.
Il segnale (fotoni, oppure e–) da un oggetto celeste in arrivo su un fotosito non cambia se le camere hanno la stessa Qe. Il flusso luminoso (fotoni/micron2*s) invece dipende anche dalle dimensioni del pixel, aumentando con la superficie di questi ultimi, e dal rapporto focale f/ del telescopio (per oggetti estesi come i pianeti, per le stelle dipende solo dal diametro dello strumento). Il segnale per un dato pixel può essere espresso anche in funzione del tempo di esposizione
Si noti che se t raddoppia, il segnale raddoppia (se siamo nel range di linearità del sensore). Dalla precente, ricordando la definizione di gain data all’inizio, segue
(con g gain effettivo che tiene conto del gain di sistema) e qui si vede che se raddoppio il gain (cioè lo aumento di 60 unità) e dimezzo il tempo di esposizione la luminosità a schermo del target (misurata con l’istogramma) non cambia.
Ora consideriamo due casi, quello in cui domina il photon noise (oggetti luminosi) e quello in cui domina il rumore di lettura.
2.1 Photon noise dominante
L’equazione per il rapporto S/N se Nr=0 si semplifica in
Quindi il rapporto segnale/rumore in questo caso (pianeti del sistema Solare, Sole, Luna, ma non Urano né Nettuno né Giove con il filtro CH4) aumenta con la radice quadrata del segnale. In altri termini, se il tempo di esposizione quadruplica, SNRframe raddoppia.
Consideriamo ora il caso, utile in pratica, dello stacking di più frames. Si sa che il SNR e la dinamica crescono con la radice quadrata dei frames sommati.
Nel caso di photon noise dominante allora per n frames
Supponiamo ora di riprendere con due tempi di esposizione, t1 e t2, con t2=1/5t1 (e quindi n2=5n1 in assenza di tempi morti). Con il tempo di esposizione più lungo, t1, si può usare un gain utente più basso di 5 volte per mantenere lo stesso segnale e quindi
Come si vede il rapporto segnale/rumore è uguale nei due casi, e quindi è indifferente usare alti gain e bassi tempi di esposizione o viceversa, se il rumore dominante è il rumore di fotoni.
2.2 Rumore di lettura dominante
In questo caso il rumore di fotoni è confrontabile con quello di lettura. I valori tipici per quest’ultimo (CMOS) sono di 3-6 e– RMS, consideriamo 4, il photon noise dovrà quindi essere sullo stesso valore (Np≈4 e– a cui corrisponde un segnale N di circa 15 elettroni). In questo caso, si può come prima diminire il tempo di esposizione per incrementare il numero n di frames (aumentando SNRstack con la radice del numero dei frames), ma il SNR del singolo frame decade rapidamente, essendo Nr indipendente dal segnale. Ricordiamo che per la linearità del sensore, il segnale diminuisce di 5 volte se il tempo di esposizione diminiusce dello stesso valore.
Supponiamo N=15 e– con t2=1/5 t1, n2=5n1 come prima.
Il SNR diventa peggiore di 2,7/1,5= 1,8 volte. Il secondo stack necessita dunque una quantità di frames sommati di 3 volte (1,8^2) maggiore per eguagliare SNR1.
La strategia migliore in questo caso è quella di porre il gain al minimo valore in cui il rumore di lettura inizia a stabilizzarsi, e settare texp massimo possibile in funzione del valore dell’istogramma desiderato e del seeing. Occorre poi integrare per un tempo più lungo possibile.
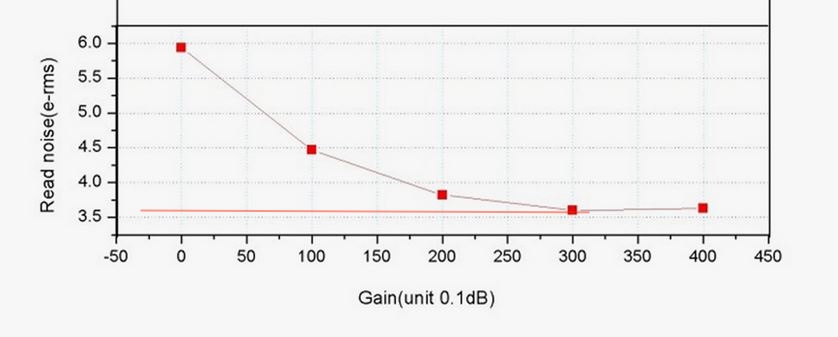
Nel caso del 174MM, come si vede dal grafico sopra il valore di gain utente dove la curva inizia ad avere derivata molto piccola è pari a circa 300. Benché l’esperienza mostri che si ottengono buoni risultati anche con valori altissimi di gain ed altrettanto lunghe integrazioni, è sempre preferibile tenere al minimo possibile il valore del gain per target poco brillanti.
3. Confronto tra sensori diversi
3.1 Caso 1: Stesso rapporto focale
In questo caso supponiamo di confrontare i sensori con lo stesso setup, o in altre parole di togliere uno e mettere l’altro al fuoco dello strumento. Entrambi i sensori ricevono naturalmente la stessa intensità F di luce. A parità di target e di texp, la luminosità B dell’immagine a schermo (misurata in ADU) aumenta con la QE e l’area del pixel (il fotosito raccoglie 4 volte più fotoni se le dimensioni raddoppiano) e diminuisce con la FWC (se raddoppia, ho un riempimento dimezzato). La FWC agisce quindi come un “serbatoio” di elettroni, e si riempie più lentamente quanto più è grande. In qualche modo controintuitivamente, i sensori con FWC maggiore danno un’immagine meno luminosa.
In formule:
dove ovviamente il confronto va fatto a parità di gain utente. F è il flusso incidente (fotoni/micron2*s). Si noti che la quantità sopra non ha unità di misura definite, e serve soprattutto a confrontare sensori differenti.
Supponiamo adesso di confrontare due sensori molto comuni ed apprezzati: il già visto IMX174MM, e l’IMX290MM.
Le dimensioni dei pixel sono qui espresse in micron.
Per la 290: B=0,8*(2,90)2 /14600 = 0,000460
Per la 174: B=0,8*(5,8)2/32400= 0,000830 (la Qe è un po’ minore della 290 a 600 nm, ma è ininfluente per il discorso).
L’immagine con la 174MM risulta più luminosa, perché la camera ha fondamentalmente pixel più grandi che compensano la maggiore FWC.
Se le due camere riprendono lo stesso pianeta, visto che la scala d’immagine o campionamento è
e la focale F non varia nei due casi, allora la scala d’immagine nei due casi avrà lo stesso rapporto delle dimensioni dei pixel. Quindi, con la 290MM, C sarà la metà (“/pix) che con il 174MM, cioè il pianeta avrà diametro doppio, in pixel.
Quindi, riprendendo lo stesso pianeta con le due camere, con il 174 sarà 8,3/4,6=1,8 volte più luminoso ed occuperà la metà delle dimensioni a schermo, tutto questo nell’ipotesi di stesso gain utente.
E il rapporto S/N? A parità sempre di gu,
Ma dalla definizione di Gain di sistema, G1/G2 è uguale a FWC1/FWC2. La relazione precedente si semplifica quindi in
Se riprendiamo un target brillante (Nr≈0), allora
e la 174MM è sempre avvantaggiata, avendo pixel di dimensioni doppie rispetto alla 290MM.
In sostanza, in caso di rapporto focale fisso, il rapporto S/N è deciso essenzialmente dalla dimensione dei pixel, e in misura minore dall’efficienza quantica che assume sempre valori molto vicini (e molto alti) per le moderne camere.
Notiamo che le considerazioni precedenti si applicano anche al binning della camera, che può essere considerato un caso particolare in cui i pixel sono uno il doppio dell’altro. Passando al bin2, il pixel di fatto quadruplica la sua superficie, raddoppiando il SNR e permettendo tempi di posa 4 volte minori.
Naturalmente, assumere rapporto focale costante non è molto realistico, perché di norma viene variato f/ con le Barlow (o, molto meno frequentemente, con riduttori) per avvicinarsi al campionamento ideale.
3.2 Caso 2: Stesso campionamento
In questo caso entrambi i sensori lavorano alle condizioni ideali di campionamento (e possono sfruttare appieno il potere risolutivo dello strumento, seeing permettendo) ma a rapporti focali diversi. Ricordando che l’f/ ideale è pari a circa 5 volte le dimensioni del pixel in micron, abbiamo che
f/1= 5*Dp1
f/2=5*Dp2, con Dp1<Dp2
con Dp dimensione del pixel (in micron). La camera sullo strumento 1 con i pixel più piccoli (lavorando a rapporto focale minore) riceverà dunque più luce nel rapporto F1/F2=(f/2 / f/1)2 =(Dp2/Dp1)2. Ricordando che i fotoni raccolti dai pixel sono invece proporzionali alle superfici di questi ultimi, e quindi quelli più piccoli raccoglieranno meno luce in proporzione a (Dp1/Dp2)2 abbiamo che i due fattori si annullano.
Il rapporto tra le due B sarà
Essendo le sensibilità dei moderni sensori CMOS molto alte ed intorno a 0,85-0,90 (peak), la differenza di luminosità dipende in questo caso essenzialmente dalla FWC. Ricordando che i pixel piccoli hanno generalmente una FWC minore, ad essi sarà associata una maggiore luminosità a schermo, che spesso viene scambiata, erroneamente, per una maggiore sensibilità.
Nel caso della 290 e della 174:
B1/B2=FWC2/FWC1=32.400/14.500=2,23.
Quindi, riprendendo lo stesso pianeta con le due camere, con la 290 sarà 2,23 volte più luminoso ed avrà le stesse dimensioni a schermo, tutto questo nell’ipotesi di stesso gain utente. In altri termini, con lo stesso tempo di esposizione e gain, il valore dell’istogramma al picco della 290 sarà 2,23 volte quello della 174.
Ricordando che B1/B2=ADU1/ADU2=FWC2/FWC1 , abbiamo
Il numero di elettroni nel well è esattamente uguale nel caso di camere usate al campionamento ideale.
Se riprendiamo un target brillante (Nr≈0), allora non solo N290=N174 ma anche SNR290=SNR174 .
Quindi in caso di campionamento ideale su target brillanti il rapporto S/N è indipendente dalla camera.
Apparentemente, la camera con pixel più piccoli avrà una sensibilità maggiore perché mostra il pianeta più brillante a parità di gain e tempo di esposizione, ma il rapporto S/N nei due casi non cambia. Invece, è la camera con i pixel più grandi a conservare un vantaggio sulla dinamica. A parità di numero di frames in stack, infatti, il rapporto S/N sarà uguale tra le due camere; però, la 174 avrà dalla sua una dinamica sul frame sempre 2,23 volte migliore in quanto avente una FWC 2,23 volte maggiore. Ne segue che la 174 richiederà lo stacking di (2,23)2=5 volte meno frames, a parità di gain e di tempo di esposizione. Questo è molto utile ad esempio nelle riprese diurne, nelle quali il seeing è fortemente variabile ed i frames di qualità accettabile sono sempre una frazione molto piccola del totale.
Visto che la luminosità a schermo è superiore, si può pensare di abbassare il tempo di esposizione della 290, aumentando l’FPS dello stesso fattore per avere lo stesso istogramma della 174. Però questo, diminuendo il segnale, peggiorerà il rapporto S/N, e dovrò sommare almeno (2,23)2=5 volte i frames per ottenere lo stesso SNR complessivo e la stessa dinamica rispetto alla 174.
4. Ricapitolazione e conclusioni
Riassumiamo qui i concetti principali esposti nei paragrafi precedenti.
- Nei sensori CMOS, non va considerato solo il gain utente, settabile, ma anche quello di sistema, impostato dal produttore e non modificabile. Il gain utente agisce come un moltiplicatore inverso, incrementado la luminosità a schermo. Il gain di sistema si legge dal grafico del gain dato dal produttore della camera, al valore di gain utente (in ascissa) pari a 0.
- Ad un incremento del gain utente di 60 unità corrisponde un raddoppio della luminosità a schermo, ad un incremento di 200 corrisponde un’amplificazione di 10 volte.
- Incrementando il gain utente, e lasciano invariati tutti gli altri parametri, nei casi ordinari di rumore di fotoni prevalente il rapporto segnale/rumore dell’immagine non cambia.
- Confrotando due camere diverse sullo stesso telescopio e con lo stesso gain utente, si confronta soltanto il rumore di lettura (che è normalmente trascurabile), che viene amplificato in funzione di gu. Il SNR infatti non dipende dal gain utente, e nemmeno il rumore termico.
- Nell’ipotesi di essere nel range di linearità del sensore, il segnale varia linearmente con il tempo di esposizione (se lo raddoppio, il segnale raddoppia). Il SNR invece varia con la radice quadrata del tempo di esposizione (se questo quadruplica, SNR raddoppia).
- Se il rumore dominante è il rumore di fotoni (caso normale nell’imaging planetario) è pressoché indifferente usare alti gain e bassi tempi di esposizione o viceversa bassi gain ed alti tempi di esposizione come strategia di acquisizione. Entrambi i metodi daranno risultati molto simili.
- Se il rumore dominante è il rumore di lettura (pianeti remoti, riprese con filtro al metano) la strategia migliore è quella di porre il gain al minimo valore in cui il rumore di lettura inizia a stabilizzarsi (vedere curve del sensore del produttore), ed integrare per un tempo più lungo possibile.
- Se si confrontano due camere differenti, accoppiandole ad un telescopio di rapporto focale fissato, il SNR dipende essenzialmente dalle dimensioni dei pixel (più grandi=SNR maggiore).
- Invece, confrondo camere differenti ma usate allo stesso campionamento, su target brillanti il rapporto S/N sul frame singolo è indipendente dalla camera. E’ dunque uguale usare (poniamo) pixel da 5 micron ad f/25, piuttosto che pixel da 3 micron ad f/15. I pixel grandi conservano però sempre un vantaggio sulla dinamica, legato alla maggiore FWC che non è scalabile.
- In definitiva, i pixel piccoli non hanno nessun vantaggio intrinseco su quelli grandi, se non quello di offrire nel caso un accoppiamento migliore con il sistema di ripresa. I pixel più grandi al contrario offrono sempre una dinamica superiore, permettendo lo stacking di un numero minore di frames a parità di tutte le altre condizioni.