Aristarco di Samo (ca. 310 a.C. circa – ca. 230 a.C.) è generalmente ricordato come uno dei pochissimi sostenitori dell’eliocentrismo nell’antichità. Tuttavia, questa notizia ci viene riportata -abbastanza vagamente- da Archimede e Plutarco, e non sappiamo molto degli argomenti che Aristarco usava per sostenere la sua ipotesi, rigettata come inutilmente artificiosa da altri sommi quali Ipparco e Tolomeo.

Di Aristarco ci è invece pervenuto intero il trattato Delle dimensioni e distanze del Sole e della Luna, si tratta di poche decine di tostissime pagine nelle quali emerge in tutta la sua bellezza il genio greco, capace di misurare il Sistema Solare con il solo potere del ragionamento.

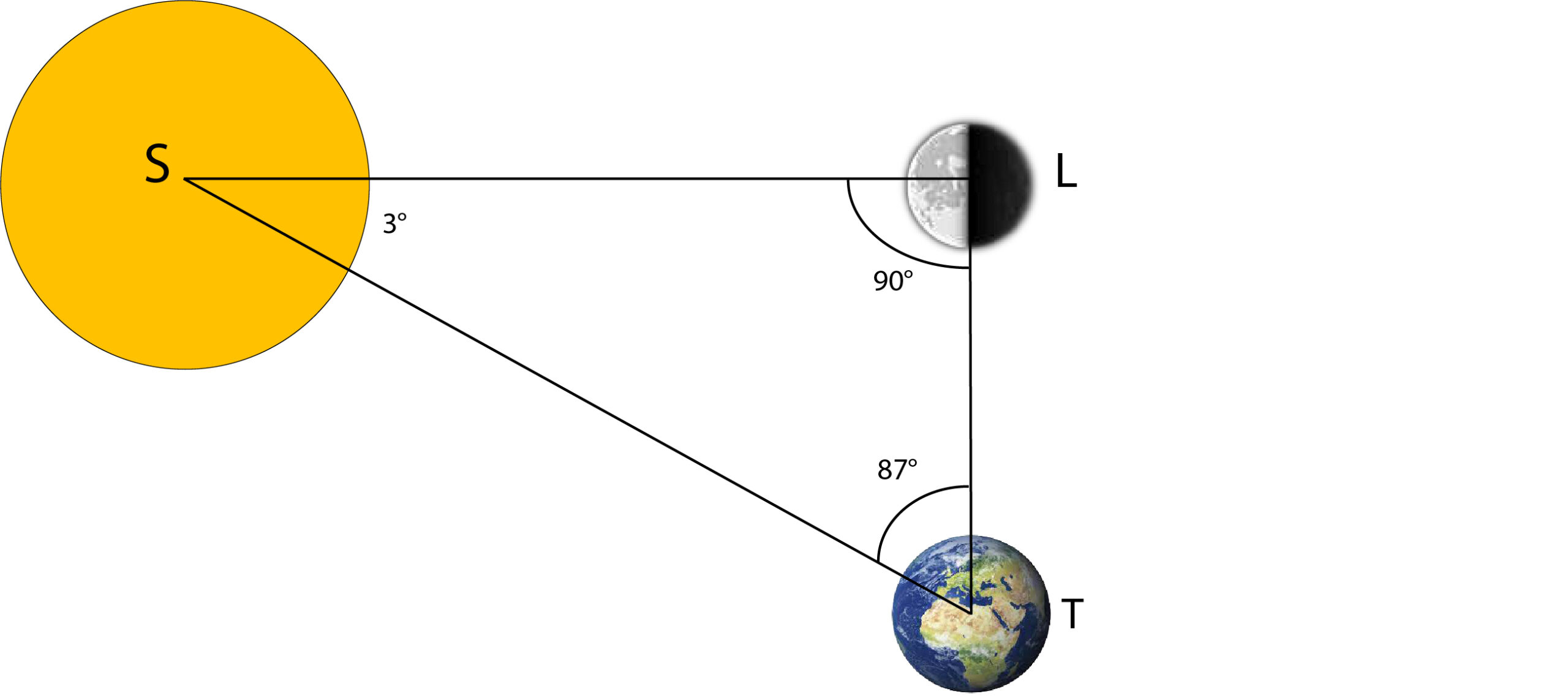
Uno degli strumenti di cui si disponeva all’epoca era la diottra, in varie versioni, che si utilizzava per misurare gli angoli. Con uno strumento simile, Aristarco aveva stabilito che quando la Luna appariva al quarto, allora dista dal Sole circa 87° (v. figura).

Ora, sfruttando una costruzione come quella della seconda figura (sostanzialmente vera anche oggi), Aristarco risolse di fatto il triangolo Sole-Terra-Luna, che dev’essere retto in L per l’ipotesi fatta di Luna in quadratura. In termini moderni, diremmo che il rapporto tra la distanza LT (Terra-Luna) e la distanza ST (Sole-Terra) è pari a sin 3°, ma Aristarco non conosceva la trigonometria (per la buona ragione che non esisteva) e attraverso tortuosi passaggi giunse a stabilire che il rapporto ST/LT era pari a circa 20. Ossia, che il Sole dista venti volte da noi più che noi dalla Luna (il valore vero è circa 400).

Il ragionamento è ineccepibile, ma risultato è errato di circa 20 volte per la difficoltà nella misura dell’elongazione lunare, che il realtà -per la grandissima distanza del Sole- è un angolo praticamente retto e pari a circa 89,5°. Né è possibile escludere che Aristarco, da vero scienziato greco, desse più importanza alle dimostrazioni che non all’accuratezza delle misure.

Ma non è finita qui: visto che dalle eclissi totali di Sole si sapeva che il diametro apparente del Sole e della Luna è circa uguale, Aristarco poteva dedurre correttamente dalla sue premesse che il Sole è circa 20 volte più grande della Luna, più di due millenni fa e senza nessuno strumento ottico.

La figura seguente è una descrizione moderna, ma rende conto delle idee alla base dei ragionamenti dell’astronomo greco, molto più complessi di quanto illustro qui.

Abbiamo visto che Aristarco stimò il rapporto dS/dL misurando la distanza angolare della Luna dal Sole alle quadrature, rapporto risultato pari a circa 20. Aristarco dovette ragionare che, finché sono nel cielo ognuno per proprio conto, era difficile comprendere le proporzioni relative di Sole, Terra e Luna, e che la chiave per avere un’idea delle loro dimensioni era sfruttare il momento preciso in cui i tre corpi celesti sono allineati: le eclissi.

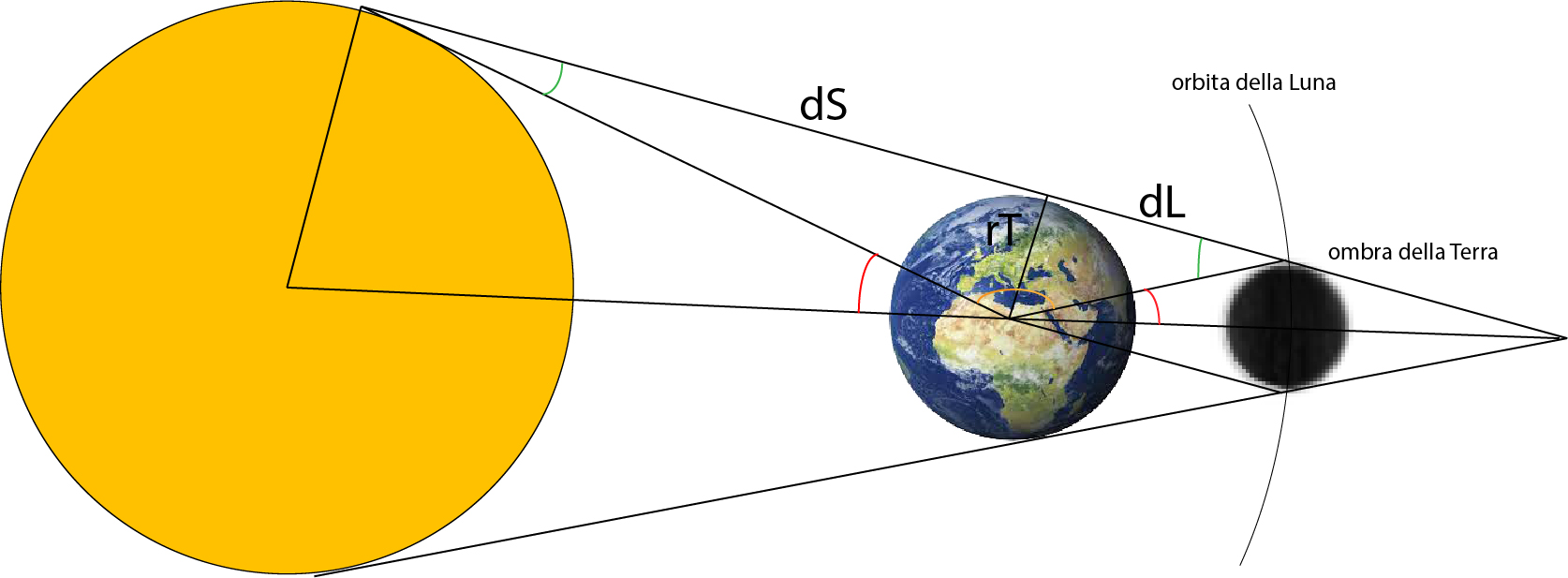
Chiunque osservi un’eclisse parziale di Luna, nota che la porzione del nostro satellite in ombra è un segmento circolare, il cui diametro angolare si può comparare alla Luna. Appunto dalle osservazioni di queste eclissi Aristarco aveva stimato che il nostro satellite era angolarmente circa la metà del cono d’ombra terrestre alla distanza della Luna. In altri termini, aveva misurato l’angolo in rosso alla destra nella figura, relativa a una eclisse lunare totale.

Ora, si sa che gli angoli in rosso, sommati, danno lo stesso valore degli angoli in verde, perché queste coppie sono entrambe supplementari dell’angolo in arancio. Visto che l’angolo in rosso a sinistra è il diametro apparente del Sole, facile da misurare, conosciamo in altre parole la somma dei piccoli angoli in verde. Non solo: conosciamo in realtà anche il loro rapporto, pari al rapporto dS/dL e dunque uguale a circa 20. Essendone noti somma e rapporto (due equazioni lineari in due incognite), abbiamo tutto quanto occorre per stimare il valore dei due piccoli angoli verdi, che sono particolarmente interessanti insieme ai due triangoli rettangoli che li contengono.

Con l’uso della trigonometria, o dei complicati passaggi di Aristarco che non la conosceva, possiamo dunque iniziare a misurare il Sistema Solare in termini di raggio terrestre, il cui valore non era ancora noto a quei tempi. In particolare, possiamo calcolare il rapporto tra dL e rT, e parimenti tra dS e rT. Finalmente, Aristarco poteva concludere che la Luna dista circa 20 raggi terrestri da noi, e il Sole circa venti volte tanto, per l’esattezza 380 raggi terrestri.

Visto che conosciamo le dimensioni apparenti, uguali, del Sole e della Luna, e le loro distanze in termini di raggio terrestre, è facile ora esprimerne anche le dimensioni in termini di raggio terrestre (e lunare). Così Aristarco tenne fede al nome del suo trattato calcolando che la Terra misura circa 2.8 raggi lunari, mentre il Sole circa 6.7 raggi terrestri.

I valori moderni sono circa 3.7 e 109, quindi mentre le dimensioni della Terra erano calcolate in modo accettabile, quelle del Sole erano gravemente sottostimate. Questo non solo per l’errore nella stima del famoso angolo di 87° di cui abbiamo parlato in precedenza (ampiamente scusabile), ma anche perché, stranamente, Aristarco stimò a 1° le dimensioni apparenti del Sole e della Luna, mentre il valore vero è circa la metà. Dico stranamente perché questo valore era abbastanza facile da misurare, anche per l’epoca.

Gli errori di misura sono tuttavia secondari nel nostro discorso, visto che il procedimento è perfettamente corretto e restituisce risultati molto più precisi se si usano in ingresso valori migliori.