Soluzione di esercizi scelti dal libro “Introduzione all’astronomia”

Questo volume, scritto dal compianto prof. Giuliano Romano e che ha avuto diverse ristampe, è da raccomandare a tutti quegli astrofili che non si accontentano della pura contemplazione del cielo stellato, e vogliono provare anche a capire quello che c’è “dietro le quinte”. Uno dei pregi maggiori del libro sono gli esercizi, utilissimi a consolidare le nozioni teoriche e a verificare la comprensione. Per essi, è generalmente riportata la soluzione ma non il procedimento per arrivarci (l’autore, in qualche caso, ne dà una traccia, altre volte la riporta per intero).

In questa pagina, presentiamo la soluzione completa della maggior parte dei problemi proposti nel libro. Lungi dall’essere fine a sé stesso, confidiamo che quanto segue possa mostrare agli appassionati come siano a portata di mano concetti considerati a torto difficili o quasi irraggiungibili, e come nello stesso tempo possano tornare utili nella pratica quotidiana dell’astronomia. Tutti i problemi presentati sono risolvibili applicando le conoscenze acquisite (dal libro o da qualunque altro testo simile di astronomia) ed il ragionamento, e richiedono al massimo l’uso della trigonometria piana; non tutti hanno, però, la stessa difficoltà.

Anche i problemi che a prima vista possono apparire solo di interesse accademico offrono in realtà sempre qualche valido spunto di riflessione.

Lista degli argomenti

Astronomia sferica

Problema 1

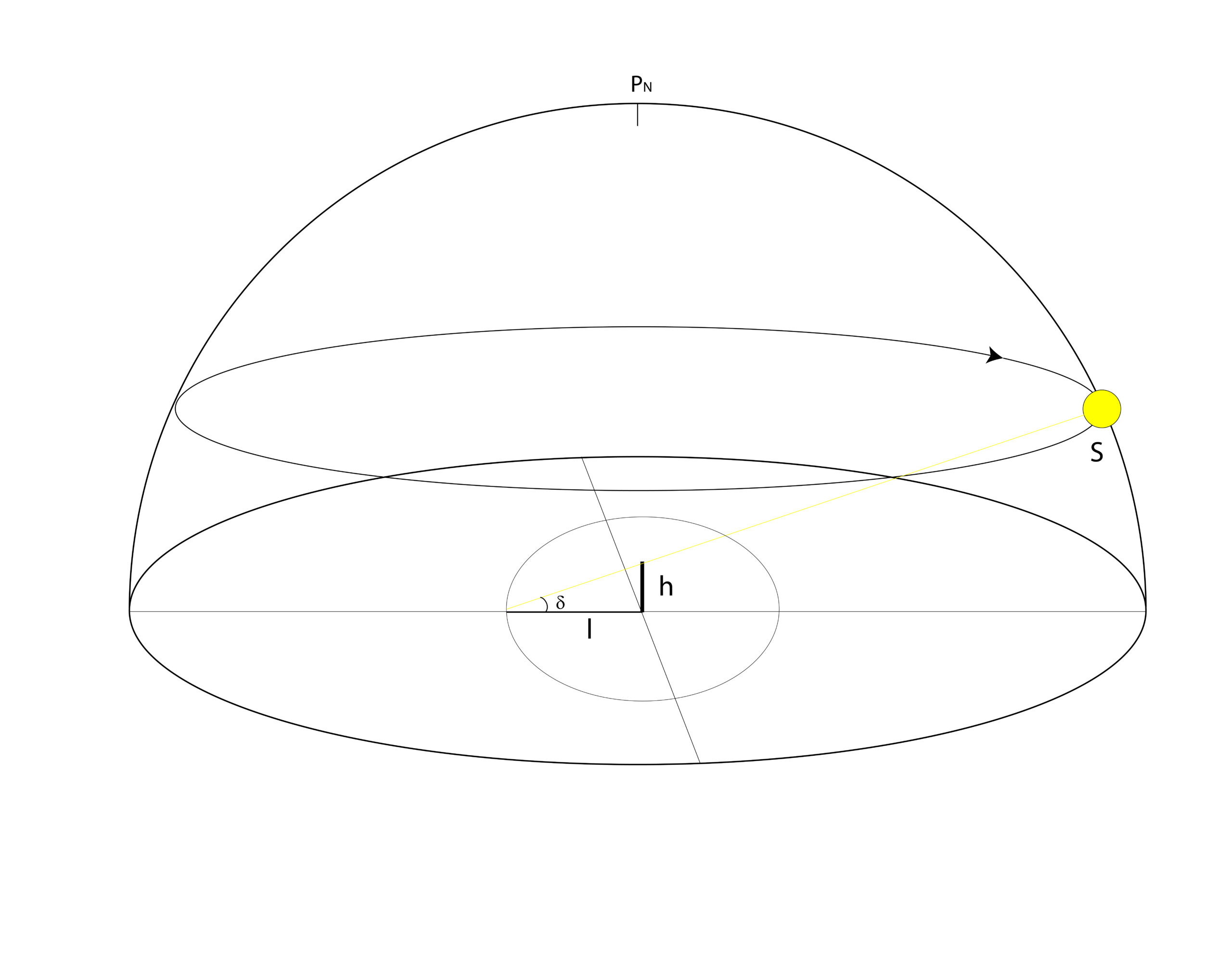
Quando Rigel (δ=-8°13′) passa alla latitudine di Roma (lat. 41°55′) a che altezza si trova sull’orizzonte?

Soluzione. Il quesito, come anche altri simili, si risolve con la relazione fondamentale riportata nel testo:

h = 90°-φ+δ

che dà l’altezza alla culminazione superiore. Sostituendo i valori (attenzione ai segni):

h = 90-41°55′-8°13’=39°52′

Notiamo che, per un dato luogo di osservazione (φ=costante) l’altezza massima aumenta con la declinazione. Quando questa raggiunge un certo valore critico, l’astro diventa circumpolare e non tramonta mai (v. problema seguente).

Si noti che la relazione presentata vale, a rigore, per la culminazione a sud dello zenit.

Problema 2

A quale latitudine si trova la città dalla quale si vede Capella (δ=+45°58′) sfiorare l’orizzonte? Non considerare la rifrazione.

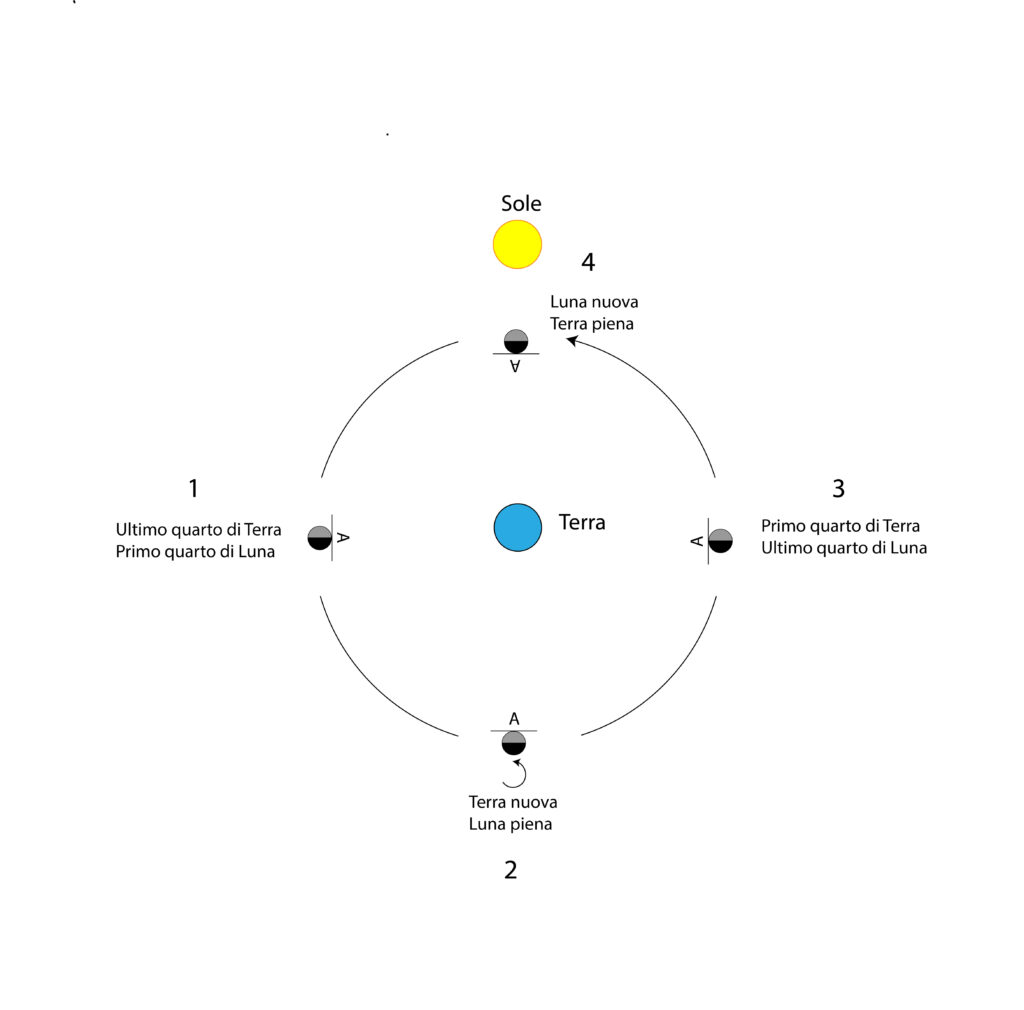
Soluzione. Ricordiamo che astri hanno in realtà due culminazioni, quella superiore (al meridiano superiore) a cui si accompagna l’altra al meridiano inferiore (culminazione inferiore). E’ possibile aiutarsi nel visualizzare cosa succede immaginando che ogni corpo celeste percorre nel suo moto sulla sfera celeste un cerchio parallelo all’equatore celeste, e che questo interseca il meridiano dell’osservatore in due punti che sono appunto le due culminazioni. Per i corpi celesti circumpolari entrambe sono visibili, mentre per gli altri è visibile solo quella superiore, o culminazione propriamente detta. Per questi astri, la culminazione inferiore avviene al di sotto dell’orizzonte visibile.

Ciò premesso, il quesito chiede a quale latitudine la culminazione inferiore di Capella sia appena sopra l’orizzonte, o in altri termini la minima latitudine da cui la stella è circumpolare. Ricordiamo che un astro è circumpolare per definizione se

δ ≥ 90° – φ

cioè se la sua declinazione è pari o maggiore alla colatitudine del luogo d’osservazione. Nel nostro caso, scriviamo

φ ≥ 90° – δ

da cui φ ≥44°2′, corrispondente all’incirca alla latitudine di La Spezia. Per luoghi di osservazione posti più a Sud, Capella non è più circumpolare, ed è osservabile sia sorgere che tramontare.

Problema 7

Trovare la massima e la minima altezza raggiunta dal Sole nella vostra città al mezzodì.

Soluzione. La declinazione massima e minima del Sole è raggiunta ai solstizi, rispettivamente estivo (δ=+23*26′) ed invernale (δ=-23*26′). I valori cercati si ricavano quindi facilmente con la relazione per la massima altezza di un astro riportata al problema 1. Per le latitudini medie italiane (42° N) l’altezza massima e minima sono pari all’incirca a 73* e 25°. In ogni caso, la differenza tra i due valori è pari a 2ε, dove ε è l’obliquità dell’eclittica (23° 26′).

Problema 10

Qual è la minima altezza di β Cas (AR=0h 8m, D=+59°) vista dalla latitudine di 45°?

Soluzione. Data l’elevata declinazione della stella, è possibile che sia circumpolare. Verifichiamolo (v. problema 2):

δ ≥ 90° – φ (condizione di circumpolarità) ⇒ 59*> 45°

quindi effettivamente β Cas è circumpolare alla latitudine indicata, che è all’incirca quella di Torino. Dal testo, sappiamo che le altezze h1 e h2 alle culminazioni rispettivamente superiore ed inferiore di un astro circumpolare sono legate alla latitudine dalla semplice relazione

φ= (h1 +h2)/2

Essendo in questo caso δ>φ, la culminazione superiore avviene a nord dello zenit (come si vede facilmente per via grafica, v. anche problema 20), e l’altezza corrispondente in questo caso è data dal complemento a 180° rispetto alla formula riportata all’es. 1.

h = 90°-φ+δ ⇒ h_circump= 180* – (90° – φ+δ) = 90*+φ -δ

e quindi per β Cas

h_circump=h1=90°+45°-59°=76°

donde finalmente

h2=2φ-h1=14°.

Problema 12

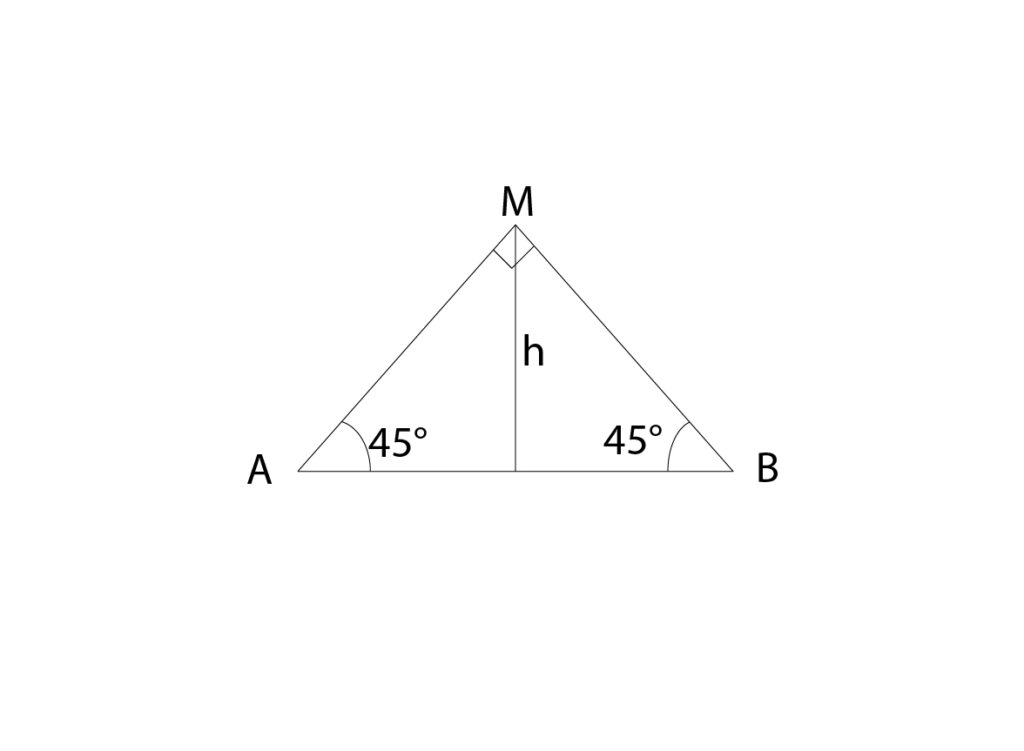
In una grande città italiana, il 13 marzo a mezzodì un’asta verticale proietta un’ombra grande quanto la sua altezza. Qual è la latitudine di questa città? La sapete individuare?

Soluzione. Facciamo riferimento alla figura sopra. Dai dati del problema, supponendo che il bastone, di lunghezza h, sia infisso in modo esattamente perpendicolare al terreno, sappiamo che il triangolo ABC è rettangolo in B, e che ha inoltre i due angoli in alfa uguali a 45° avendo uguali i due cateti. Conosciamo dunque l’altezza del Sole nel luogo considerato, al mezzogiorno. Il giorno 13 marzo, la declinazione del Sole è facilmente ricavabile dalle tavole riportate nel libro (o anche da altre effemeridi) e risulta pari a -3° 5′. Poiché siamo al mezzodì (vero, non quello dell’orologio!) l’altezza del Sole in quel momento si ricava dalla relazione già più volte utilizzata

h = 90°-φ+δ

da cui

φ= 90°+δ-h=90°-3°5′-45°=41°55′

L’unica grande città italiana a questa latitudine è Roma.

Problema 13

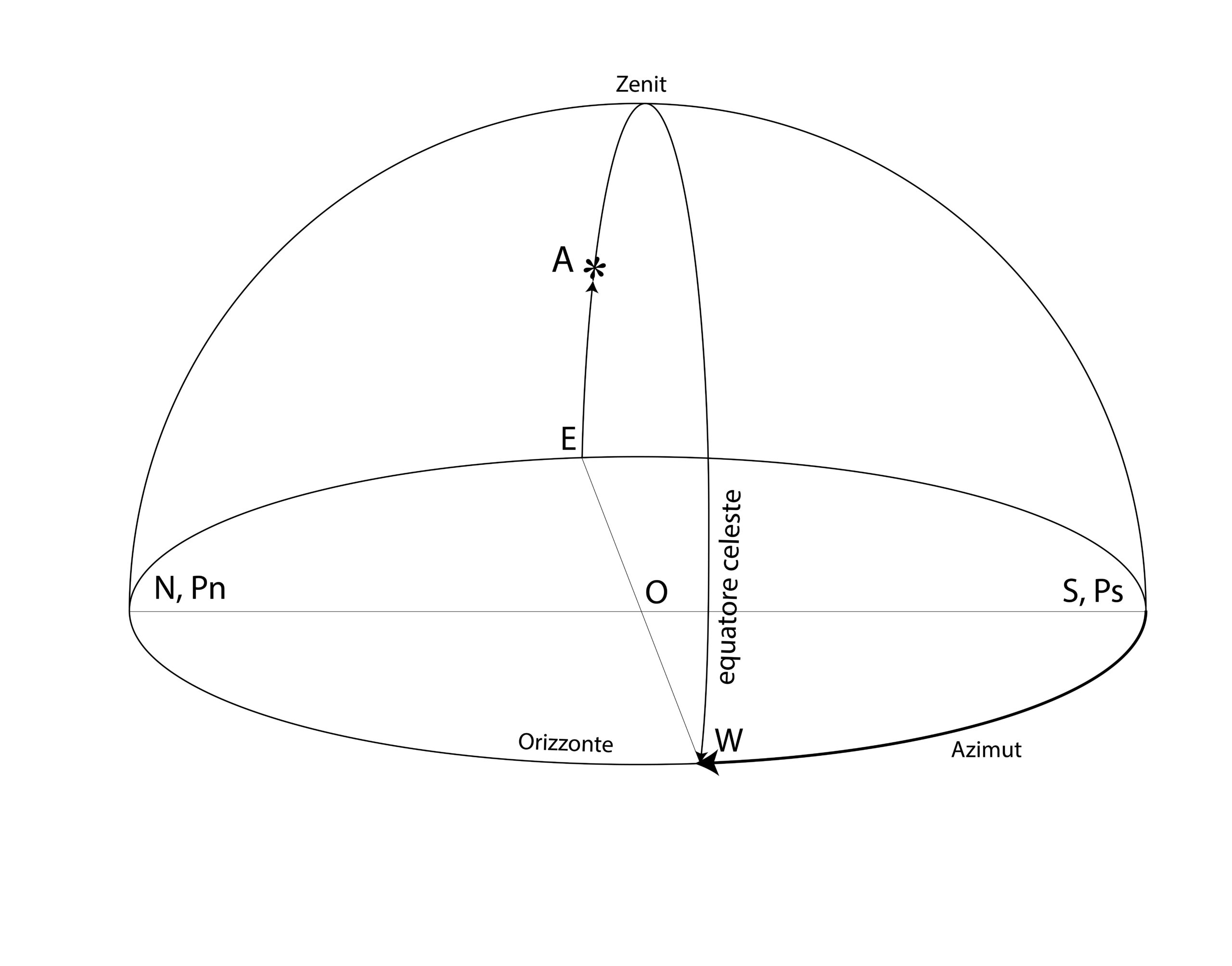
Quale declinazione deve avere una stella e da quale latitudine deve essere vista affinché il suo azimut non cambi dal sorgere fino al passaggio al meridiano?

Soluzione. Il problema si può risolvere per via analitica con le equazioni dell’astronomia sferica, che sono piuttosto complesse. Conviene adottare una risoluzione grafica; a tal fine facciamo riferimento alla figura sotto.

Sappiamo che il luogo dei punti in cui l’azimut è costante è un cerchio verticale, ossia un cerchio massimo passante per lo zenit e l’astro considerato, e contenente la verticale dell’osservatore (misuriamo l’azimut secondo la convenzione astronomica, da Sud verso Ovest). Però gli astri si muovono sui paralleli di declinazione, ovvero su cerchi paralleli all’equatore celeste. L’unico caso in cui un parallelo di declinazione possa coincidere con un cerchio verticale si ha quando detto parallelo contiene la verticale per l’osservatore, il che può accadere solo all’equatore (v. figura, dove è rappresentata la sfera celeste per un osservatore O posto a latitudine zero). In questo caso (e solo in questo), i poli celesti Pn, Ps giacciono sull’orizzonte e il piano dell’equatore celeste è perpendicolare all’orizzonte. Un astro A con declinazione pari a zero si muove quindi in contemporanea sull’equatore celeste e sul primo verticale (ovvero il cerchio verticale passante per i punti cardinali E ed W), mantenendo dopo il sorgere azimut costante pari a 270°. Dopo la culminazione, l’azimut “salta” a 90°.

Problema 14

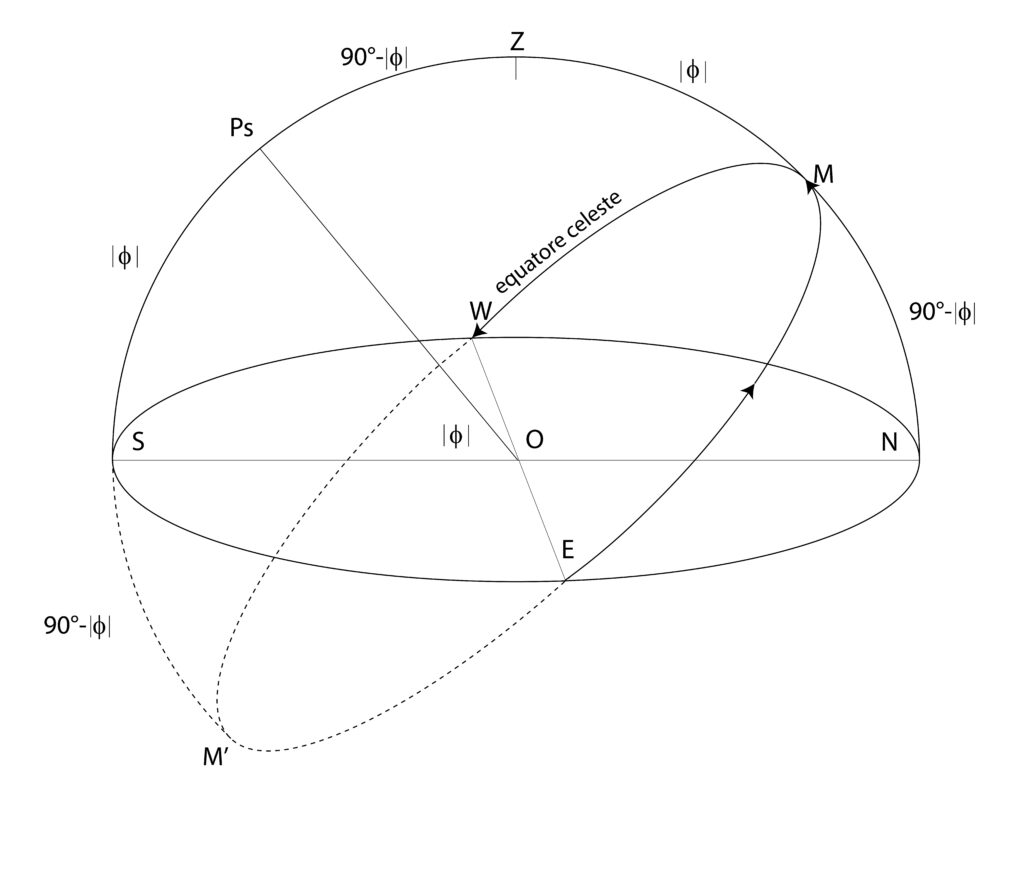
Quali sono le coordinate orarie per un osservatore posto nell’emisfero australe dei 4 punti cardinali e dello zenit? Disegnare la volta celeste e i 4 punti cardinali.

Soluzione. Il problema è molto interessante per approfondire il moto apparente sulla sfera celeste nell’emisfero sud. Si faccia riferimento alla figura sotto, che rappresenta la volta celeste per un osservatore O alle medie latitudini australi.

Il moto degli astri avviene sempre da E verso W, ma nel senso diretto (antiorario), cioè l’opposto di quanto accade nel nostro emisfero. Inoltre, gli astri culminano superiormente a nord e non a sud. Quanto detto ha conseguenze su come si computa l’angolo orario: infatti, questo segue il moto apparente degli astri, e quindi nell’emisfero australe si misura da nord verso ovest (nell’emisfero nord si misura da sud verso ovest). Tutto ciò premesso, indicato con |φ| il valore assoluto della latitudine del luogo d’osservazione supposta negativa, possiamo derivare alcuni angoli notevoli indicati in figura. Ps è il polo sud celeste, lo zenit è in Z, M sia il mezzocielo superiore, M’ quello inferiore (sotto l’orizzonte). L’orizzonte contiene i quattro punti cardinali N, S, E ed W. Gli elementi della sfera celeste al di sotto dell’orizzonte, invisibili. sono indicati con linea tratteggiata.

La distanza Ps-Z è pari naturalmente a 90°-|φ|, poiché ZS è retto. Dunque anche ZM è noto e pari a |φ| perché complementare di Ps-Z. Con ragionamenti analoghi, ricaviamo l’angolo MN pari a 90°-|φ| così come l’angolo M’S. Osserviamo che gli astri a sud dell’equatore celeste (ovvero verso l’alto, nel disegno) hanno declinazione minore di zero.

Finalmente, deduciamo le coordinate orarie dei 4 punti cardinali e dello zenit.

S: H=12h; δ=-(90°-|φ|) = -90*+|φ|= -90*-φ= -(90°+φ)

N: H=0H; δ= 90°+φ (i punti cardinali N ed S hanno declinazioni opposte)

E: H=18h; δ=0°

W: H=6h; δ=0°

Z: H=0h; δ=φ

Problema 20

In quale epoca e a quale ora un’asta verticale posta sul tropico del Capricorno non proietta ombra?

Soluzione. Al tropico del Capricorno la latitudine è φ=-23°26′. Se l’asta non proietta ombra, allora il Sole dev’essere al culmine della sfera celeste, allo zenit, in un istante che non può essere che il mezzodì (h=90°). Poiché al momento della culminazione vale la relazione già incontrata

h = 90°-φ+δ

sostituendo i valori e risolvendo per δ troviamo δ=φ=-23°26′. Siamo pertanto al solstizio invernale.

Al tropico del Cancro (φ=+23°26′) capita naturalmente lo stesso fenomeno, ma al solstizio estivo.

Si vede dalla relazione precedente che h=90° se e solo se φ=δ. Il problema proposto è dunque un caso particolare della proposizione secondo cui un corpo celeste culmina allo zenit solo quando la sua declinazione è uguale alla latitudine del luogo d’osservazione. Poiché la declinazione del Sole varia come sappiamo da +23°26′ a -23°26′, segue che esso può culminare allo zenit solo per luoghi posti tra i tropici.

Problema 23

Per un osservatore posto nell’emisfero boreale, la stella Aldebaran (AR 4h 34m) si trova nella parte Est o quella Ovest del cielo quando il punto gamma passa al meridiano superiore?

Soluzione. Per definizione, l’angolo orario del punto gamma è pari al tempo siderale; quindi, quando esso culmina, il tempo siderale è zero e in quell’istante transitano al meridiano gli astri con AR=0. Poiché le ascensioni rette crescono seguendo il moto apparente del Sole tra le stelle (quindi verso Est), Aldebaran si trova ad Est del meridiano.

Una soluzione più analitica si può ottenere ricordando la definizione di tempo siderale (TS):

TS=AR+H

con AR ascensione retta dell’astro considerato ed H il suo angolo orario. All’istante della culminazione del punto gamma, TS=0 e H=-4h 34m, sicché Aldebaran si trova ad Est del meridiano per definizione di angolo orario.

Problema 26

Verso quale periodo dell’anno la stella Sirio (AR=6h 44m) culmina a mezzanotte?

Soluzione. Gli astri culminano a mezzanotte quando sono in opposizione al Sole; cioè in questo caso quando il Sole ha AR=12h+6h 44m=18h 44 m. Sapendo che il Sole transita al punto vernale all’equinozio di primavera (AR=0), e che in un mese percorre 24/12=2h di AR sull’eclittica nel senso diretto (antiorario), segue che il momento dell’opposizione di Sirio avverrà all’incirca due mesi e mezzo prima dell’equinozio, cioè all’inizio di gennaio.

Interessante notare come la posizione dell’osservatore non sia rilevante in questo problema.

Problema 30

A quale latitudine Canopo (D=-52°40′) comincia ad essere appena visibile all’orizzonte?

Soluzione. Si chiede in altri termini la latitudine alla quale la stella culmina superiormente ad h=0° (si ignora la rifrazione). Si applica la relazione

h = 90°-φ+δ

da cui φ=37° circa. Canopo è dunque teoricamente visibile dall’estremità meridionale della Calabria e dalla Sicilia.

Problema 32

Se in un dato giorno una stella passa al meridiano superiore alle 23, a quale ora vi passerà un mese dopo?

Soluzione. Il giorno siderale, ovvero il tempo che le stelle fisse impiegano per fare un giro completo sulla sfera celeste, dura 4 minuti in meno di quello solare, cioè 23h 56m; ne segue che una data stella anticipa il proprio passaggio al meridiano di 4 minuti ogni giorno, o 2h al mese. L’astro culminerà perciò alle 21.

Problema 35

In quale istante di tempo siderale la stella Castore (AR=7h 33m 31s; D=31°55’35”) è alla culminazione inferiore, e quale altezza ha sull’orizzonte per un osservatore posto alla latitudine 65°N?

Soluzione. Anzitutto osserviamo che la stella è circumpolare alla latitudine specificata, essendo δ > 90° – φ. La sua culminazione inferiore avviene a nord, ed il suo angolo orario H in quell’istante sarà pari a 12h. Poiché TS=AR+H, si ha subito

TS = 7h 33m 31s+12h = 19h 33m 31s

Per l’altezza h2 alla culminazione inferiore usiamo per semplicità la relazione (non riportata nel testo, comunque derivabile agevolmente per via grafica)

h2 = δ + φ – 90°

da cui h2=6° 55′.

Problema 36

Quale curva descrive l’ombra di uno stilo verticale posto al polo nord il 21 giugno? Quale è il rapporto tra la lunghezza l dell’ombra e l’altezza h dello stilo?

Soluzione. La sfera celeste vista dai poli terrestri così come il moto apparente degli astri su di essa è del tutto peculiare (v. figura).

Il Polo celeste (in questo caso quello Nord, Pn) si trova allo zenit, e l’equatore celeste coincide con l’orizzonte. Tutti gli astri sono circumpolari; nessuno di essi sorge né tramonta, per cui non sono definiti né l’Est né l’Ovest. Al solstizio estivo, il Sole percorre il parallelo celeste descritto in figura, e poiché l’orizzonte coincide con l’equatore celeste, l’altezza è pari alla sua declinazione:

h = δ = 23°26′

Siccome l’altezza del Sole non cambia durante il solstizio, l’ombra proiettata al suolo ha sempre la stessa lunghezza e la figura descritta dalla sua punta è un cerchio (normalmente è un’iperbole). Il rapporto h/l come si vede dal disegno è pari a tan 23°26’=0.43.

Dopo il solstizio, il Sole comincia ad abbassarsi sull’orizzonte, mantenendo sempre un’altezza costante per un dato giorno pari alla propria declinazione e descrivendo una lenta spirale, che dura 6 mesi. All’equinozio (δ=0°) l’astro raggiunge finalmente l’orizzonte, dando inizio ai 6 mesi di buio.

Problema 40

I cinesi, nel 1100 a. C., avevano trovato che a mezzodì l’altezza del Sole era 79°7′ al solstizio estivo, e 31°19′ in quello invernale. A quale latitudine hanno fatto l’osservazione, e qual era allora l’obliquità dell’eclittica?

Soluzione. La declinazione del Sole varia da -ε a +ε ai due solstizi, dove quest’angolo (in valore assoluto) è pari all’obliquità dell’eclittica che varia lentamente nei secoli. In questo esercizio, diversamente dai precedenti, l’obliquità dell’eclittica è incognita. Al solstizio estivo si ha

h1 = 79°7’= 90°-φ+ε

mentre in quello invernale

h2 = 31°19’= 90°-φ-ε

Le due equazioni formano un sistema lineare di due equazioni in due incognite, che si può risolvere ad esempio sommandole membro a membro ottenendo

79°7’+31°19’=180°-2φ

da cui

φ= 34°47′

e quindi ε=23°57′.

L’obliquità dell’eclittica era dunque mezzo grado maggiore dell’attuale (23°26′).

Problema 41

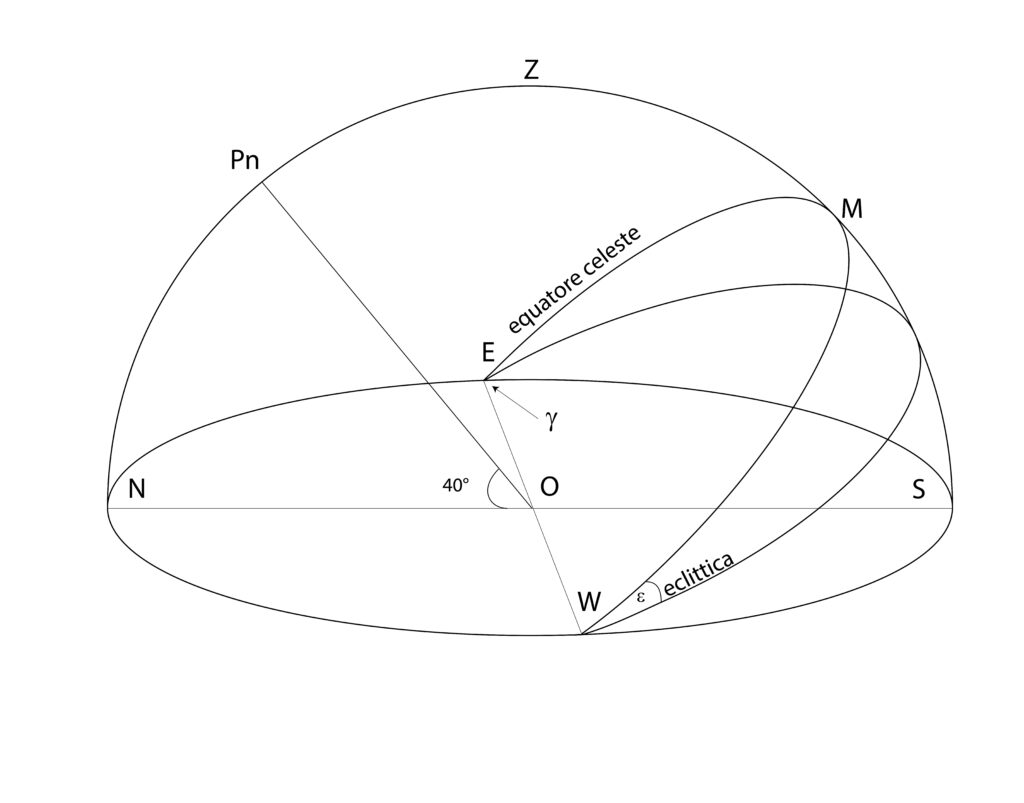
Calcolare approssimativamente l’angolo tra l’orizzonte e l’eclittica nel momento in cui il punto gamma sorge all’orizzonte avendo l’azimut di 90° ad Est del Nord, per un luogo di latitudine 40° N.

Soluzione. Consideriamo la figura seguente, che rappresenta la sfera celeste per un osservatore posto alla latitudine di 40°N.

L’osservatore sia in O, e lo zenit in Z. L’altezza del Polo Nord celeste Pn è uguale alla latitudine, mentre si vede facilmente che (essendo l’equatore celeste perpendicolare all’asse del mondo O-Pn) l’angolo MS è pari a 90°-40°= 50°. Infatti, l’angolo PnM è retto, dunque PnN+MS è retto anch’esso, da cui MS=50°. E’ noto che l’inclinazione ε dell’eclittica sull’equatore è pari a 23°26′ (obliquità dell’eclittica) e che l’equatore stesso interseca l’orizzonte nei punti cardinali E ed W.

Il problema è complicato dal fatto che l’eclittica, pur mantenendo un angolo costante con l’equatore celeste fisso, varia continuamente la sua inclinazione rispetto all’orizzonte, sia durante il giorno che durante l’anno. Per fissare la sua posizione all’istante considerato, si consideri quanto segue:

1) il punto gamma (uno dei due punti d’intersezione tra equatore ed eclittica) sta sorgendo ad Est, quindi per questo punto cardinale passano eclittica, equatore ed orizzonte nel momento considerato;

2) il Sole si muove sull’eclittica nel senso diretto (da W ad E), dunque la parte visibile dell’eclittica deve necessariamente trovarsi al di sotto dell’equatore celeste perché il Sole deve avere declinazione positiva dopo l’equinozio di primavera (o, equivalentemente. deve avere declinazione negativa prima). Si ricordi che il moto apparente del Sole si svolge, per definizione, sull’eclittica.

Determinato univocamente, in tal modo modo, l’aspetto della sfera celeste, l’angolo tra eclittica ed orizzonte si calcola agevolmente dal disegno essendo pari a MS-ε= 26°33′.

Il tempo

Problema 44

Alle 20 del 2 marzo a che h siderale corrisponde?

Soluzione. Si intende a Greenwich, per cui vale la tabella a pag. 48 della 3a edizione che riporta il tempo siderale alle 0 TU del 2 marzo, pari a 10h 37m. Dobbiamo aggiungere a questo tempo 20 h medie, pari a circa 20+ (20/24)*4= 20h 3m siderali. L’ora richiesta è dunque

10h 37m+20h 3m=6h 40m

Problema 46

Qual è l’ora siderale approssimata relativa al 1 gennaio alle 9 del mattino, a Greenwich?

Soluzione. Dalla tabella a pag. 48 ricaviamo che a Greenwich, alla mezzanotte civile del 1 gennaio, il tempo siderale è 6h 40m. Dobbiamo quindi aggiungere 9 ore civili, pari a 9+(9/24)*4=1.5 minuti siderali, che arrotondiamo a 1. Otteniamo

6h 40m+9h 1m=15h 41m

Problema 46

Adoperando un almanacco, calcolare il tempo siderale corrispondente alle 13h 25m di tempo medio (del fuso), del 14 maggio 1983 in una località la cui longitudine è 0h 48m Est.

Soluzione. Ricordiamo che quando l’orologio al sito indicato segna le 13:25 (tempo medio del fuso o tempo civile, per definizione), a Greenwich l’orologio segna le 12:25. Trascuriamo l’ora legale in questo problema e proponiamo una soluzione che metta in risalto i ragionamenti implicati (il testo di Romano dà semplicemente la formula risolutiva).

In questo tipo di calcoli, si parte sempre dal tempo siderale di Greenwich, che è tabellato. Alla mezzanotte (civile) del 13 maggio il TS a Greenwich è pari a 15h 21m; occorre aggiungere quindi 24h+12h 25m=36h 25m civili, per ottenere il tempo siderale alla data indicata. Convertiamo singolarmente i due addendi:

1) 24h civili sono pari a 24h 4m siderali;

2) 12h 25m=12,41h civili danno 12h+(12,41/24)*4=12h 27 m circa siderali.

Dunque 36h 25m civili sono pari a 36h 31m siderali, che corrispondono a 1g 12h 31m siderali. Concludiamo che il tempo siderale a Greenwich alla data indicata sarà 15h 21m + 1g 12h 31m = 3h 53m.

Se visualizziamo questo tempo siderale come l’angolo orario del punto gamma (che si può assimilare a una stella fissa), è facile capire che spostandosi in longitudine ad Est od Ovest il punto gamma si sposta in accordo, verso occidente od oriente rispettivamente (pensiamo che spostandosi ad E l’ora aumenta, e gli astri si spostano verso il tramonto). Dunque, poiché osserviamo a 48m di distanza ad Est di Greenwich il tempo siderale sarà

3h 53m + 48m = 4h 41m

Problema 50

In una città posta sull’equatore, una piazza circolare ha diametro di 300 m. Che differenza di tempo si misura nel passaggio del Sole al meridiano visto dai due estremi della piazza?

Soluzione. Il problema richiede, in altri termini, il tempo che il Sole impiega ad attraversare la piazza. Assumiamo il raggio equatoriale R_eq terrestre pari a 6371 km. La circonferenza sarà 2πR_eq = 40.010 ≃ 40.000 km. Possiamo impostare la proporzione (con x il tempo richiesto):

24h:40.000 = x:0,3

da cui x=0,6 sec.

Problema 52

Una stella, osservata a Greenwich in un certo istante, ha angolo orario pari a 5h 27m; osservata invece in una località A, nello stesso istante, il suo angolo orario è pari a 3h 40m. Qual è la longitudine di A?

Soluzione. Come è dimostrato graficamente nel testo, la differenza tra gli angoli orari è pari alla differenza di longitudine tra i luoghi:

H_A-H_G= λ_A-λ_G

con λ_G=0. Quindi, ricordando che le longitudini sono positive verso E:

λ_A=3h 40m-5h 27m=1h 47m W

Problema 54

Gli antichi Egizi stabilirono l’inizio dell’anno al sorgere eliaco di Sirio (Sothis). Poiché essi adottarono l’anno vago di 365 giorni, ogni anno Sirio sorgeva leggermente in ritardo. Dopo quanti anni (periodo sotiaco) Sirio torna a sorgere nella stessa stagione?

Soluzione. Adottiamo per la durata dell’anno siderale il valore di 365 h 6h. Sirio sorgeva dunque con 6h di ritardo ogni anno vago, ossia un giorno ogni 4 anni vaghi. Per completare un giro completo della volta celeste occorrevano dunque 4×365=1460 anni.

Problema 55

Una città A è posta alla longitudine 43° 12′ E di Greenwich. Quando in A l’orologio segna le 20h 35m siderali, in un’altra città B l’orologio segna le 23h 12m siderali. Qual è la longitudine di B?

Soluzione. Riguardiamo, come già fatto (v. problemi 46 e 52) i tempi siderali come angoli orari. Spostandosi in longitudine ad Est, gli astri si spostano ad Ovest, l’angolo orario cresce e così il tempo siderale. Dunque B si trova 23h 12m-20h 35 m= 2h 37m più ad E rispetto ad A. Poiché 365 gradi di longitudine equivalgono a uno spostamento di 24h, allora 15 gradi di longitudine equivalgono ad un angolo orario di 1 ora, e 2h 37m equivalgono a 2,56h*15°= 39.25°= 39°15′. La longitudine di B è

λ_B= 43° 12′ + 39°15′ = 82°27′ E

Problema 56

Sull’almanacco astronomico si trova che il 25 giugno 1983 vi fu una eclisse di Luna, e il primo contatto dell’astro con l’ombra della Terra avvenne alle 7h 15m TU. Un osservatore in una certa città posta a latitudine -20° notò che il fenomeno si era verificato alle 4h 19m ora locale. Qual è la longitudine e il nome della città?

Soluzione. L’unica difficoltà del problema consiste nel notare che l’osservatore misura il tempo medio locale, non il tempo medio del fuso come usuale (che è il tempo dell’orologio). In questo caso è immediato ricavare la longitudine dell’osservatore con una semplice differenza:

7h 15m-4h 19m= 2h 57 m

Poiché vale l’equivalenza 15°=1h, allora 2h 57 min=2,95h equivalgono a 2,95*15=44.25°=44° 15′. L’osservatore si trova ad W di Greenwich, visto che il suo tempo è precedente, dunque la sua longitudine è circa 44°. L’unica grande città che ha questa longitudine e latitudine -20° è Belo Horizonte, in Brasile.

Antichi metodi elementari per la misura del raggio terrestre

Problema 68

Se passando dal luogo dove si vedono tutte le stelle circumpolari a quello in cui non se ne vede nessuna si percorrono 10.018 km, quanto misura il raggio terrestre?

Soluzione. Dai Poli nessuna stella è circumpolare, dall’equatore tutte (v. problemi 13 e 36). La distanza percorsa (supponendo di procedere lungo un meridiano) è quindi 1/4 della circonferenza terrestre, e si può scrivere

(2πRt/4) = 10.018

da cui Rt=6380 km. Si noti che la Terra è supposta sferica.

Problema 70

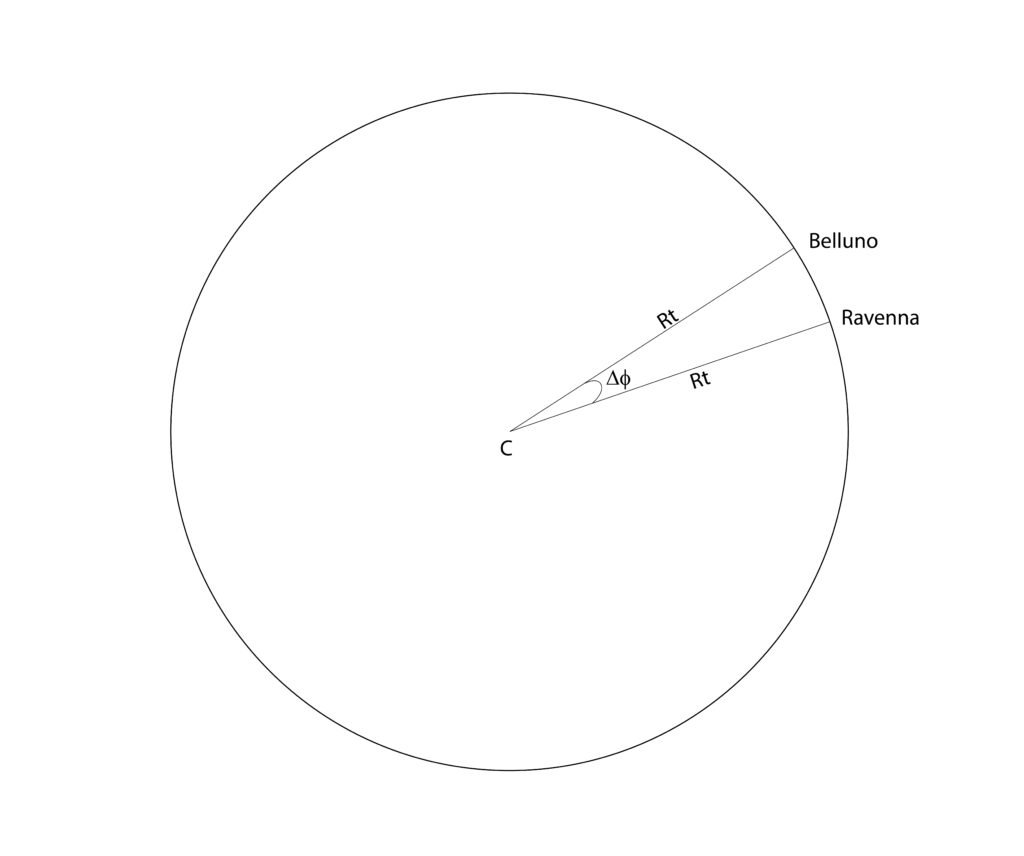
Supposta la Terra sferica con R=6378 km, quale distanza intercorre tra Belluno (φ= 46° 8′) e Ravenna (φ= 44° 25′) che sono poste sullo stesso meridiano?

Soluzione. Riferiamoci alla figura seguente, in cui è rappresentato il meridiano passante per Belluno e Ravenna. Il centro della Terra è in C e Rt è il raggio terrestre. L’angolo Δφ rappresenta la differenza tra le latitudini delle due città, che è nota.

L’arco di circonferenza tra Belluno e Ravenna si calcola agevolmente come Rt*Δφ se si esprime Δφ in radianti. Poichè 1 rad=57,3° e Δφ= 1° 43′ = 1.72°, allora Δφ=0.03 rad e la distanza cercata è 6378*0.03=191 km.

Problema 71

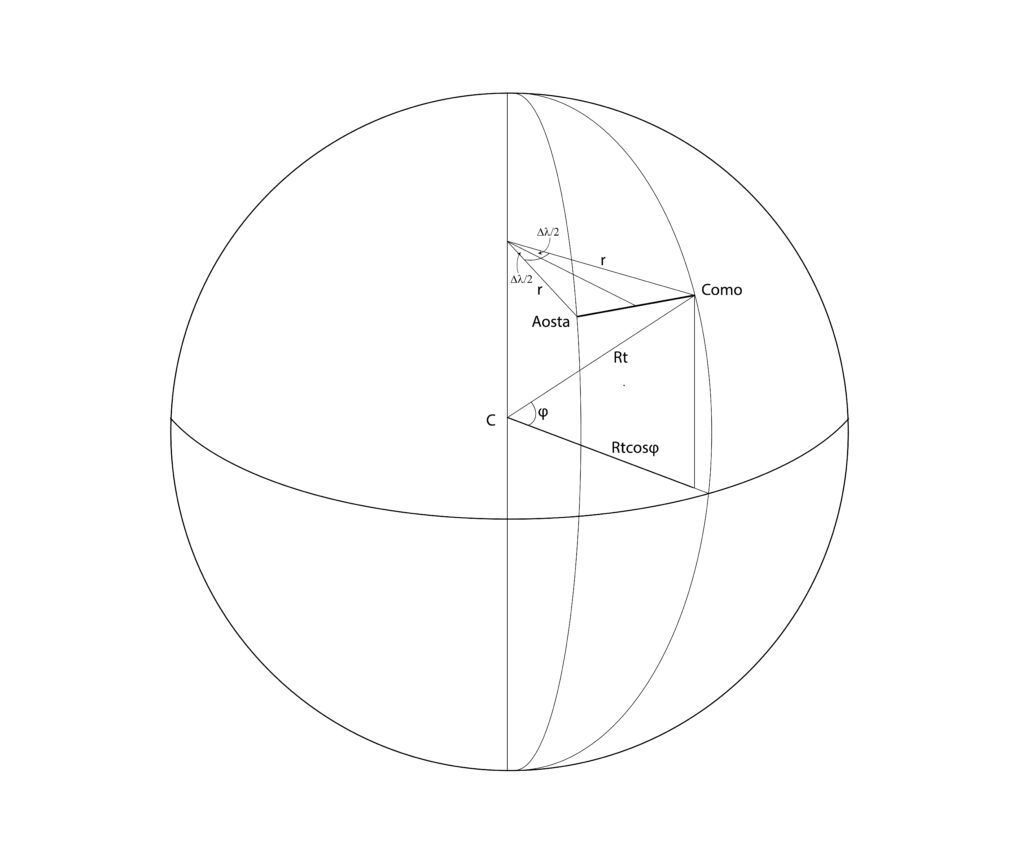
Aosta (φ= 45° 44′; λ=-0h 29m 16s) e Como (φ= 45° 47′; λ=-0h 36m 20s) sono pressappoco sullo stesso parallelo; quanti km distano in linea d’aria?

Soluzione. Riferiamoci alla figura sottostante, in cui è rappresentata la sfera terrestre con raggio Rt e centro C, e i meridiani passanti per Aosta e Como. E’ rappresentato, in linea spessa, anche l’equatore.

Si vede dalla figura che il raggio terrestre r alla latitudine delle due città è pari a Rt*cosφ=4452 km. La distanza in linea d’aria richiesta sarà allora data da 2r*sin (Δλ/2), dove Δλ è la differenza di longitudine delle due città.

Δλ= 0h 36m 20s – 0h 29m 16s= 7m 4s = 7,07m = 0.118h = 1.77°

e quindi la distanza d richiesta è pari a

d= 2*4452*sin (0.88°)= 137 km

Problema 72

Nel problema precedente, qual è la distanza d’arco tra le due città?

Soluzione. Il prodotto r*Δλ rappresenta evidentemente la distanza d richiesta (con Δλ in radianti). Si ha

Δλ=1,77°=0,031 rad

e

d= 4452*0,031=138 km

Si noti che la relazione precedente 2r*sin (Δλ/2) si riduce a r*Δλ ricordando che abbiamo a che fare con angoli piccoli (<2°) per i quali vale l’approssimazione sin λ ≈ λ, con λ in radianti.

Problema 73

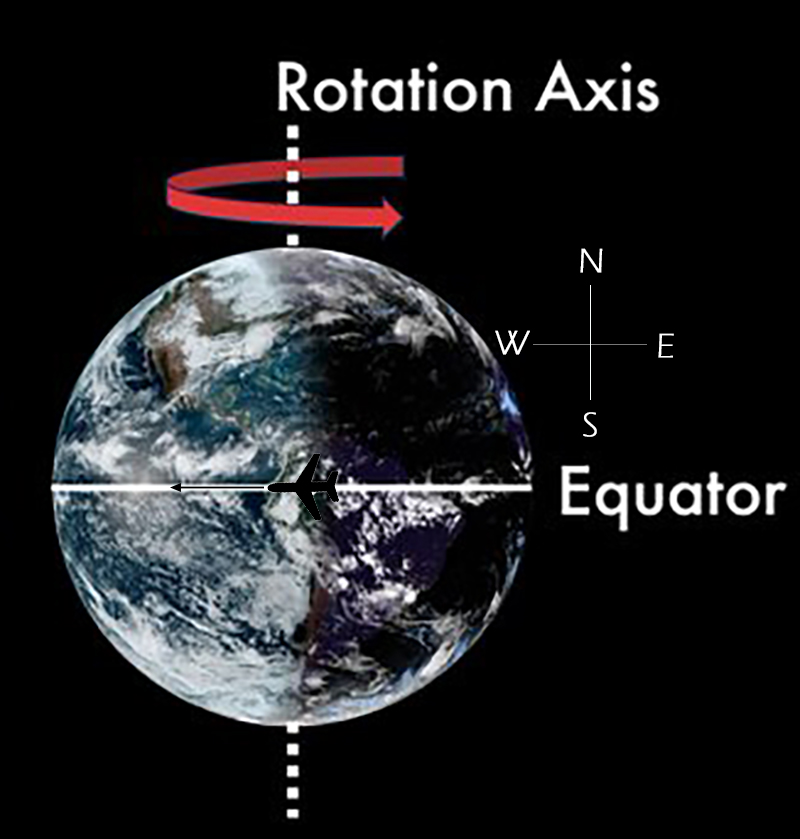
Se viaggiando in aereo lungo l’equatore verso Ovest si inizia il viaggio al tramonto del Sole, quale velocità deve avere l’aereo per vedere il Sole sorgere ad Ovest, anziché tramontare da quella parte?

Soluzione. La situazione iniziale è illustrata nella figura sottostante (crediti NWS).

La Terra ruota da Ovest verso Est, per questo gli astri sembrano muoversi nel senso opposto, da Est ad Ovest. Un osservatore che si trovi nei pressi del terminatore, sulla parte illuminata, si sposta verso oriente e vede dunque il Sole tramontare.

Il terminatore, rispetto alla superficie terrestre, si muove verso Ovest ad una velocità v calcolabile come il rapporto tra la circonferenza terrestre equatoriale Req (circa 6380 km) e il giorno siderale (24h):

v= (2πR_eq)/24=1670 km/h

che naturalmente è anche la velocità di rotazione terrestre. Se l’aereo si muove ad una velocità appena superiore a questa, sempre verso occidente, comincerà a precedere il terminatore finché a un certo punto lo incontrerà nuovamente per due volte, vedendo la seconda il Sole sorgere ad Ovest (fig. sotto).

Problema 74

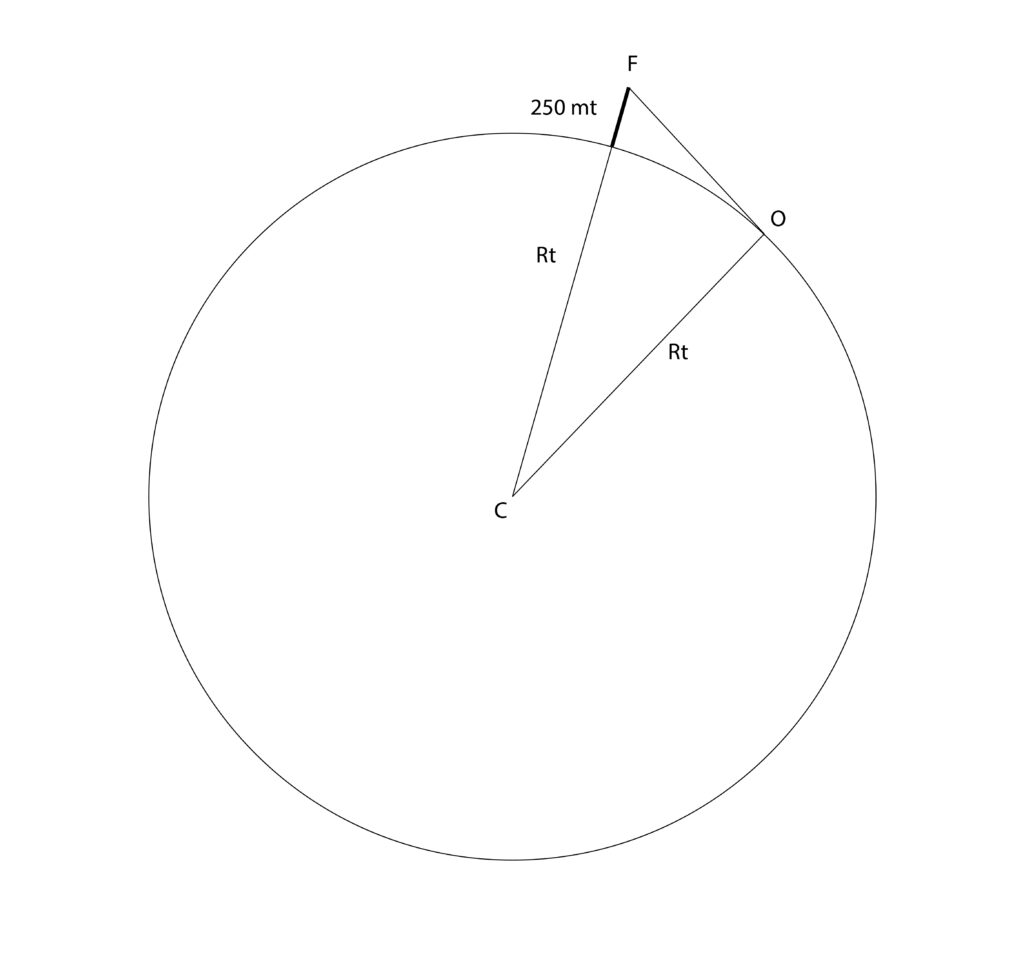
Fino a quale distanza si vede un faro alto 250 m sul livello del mare?

Soluzione. Consideriamo la figura sottostante, che mostra il meridiano passante per un osservatore O ed il faro. Evidentemente, a causa della curvatura terrestre, la distanza OF è la massima a cui è possibile vedere il faro. Il triangolo COF è retto in O, per cui si ha dal teorema di Pitagora (Rt=6380 km)

(Rt+0,250)²=OF²+Rt²

da cui ricaviamo OF= 56 km. Si noti che la formula sopra restituisce anche la distanza dell’orizzonte per un osservatore elevato di un’altezza F rispetto al suolo.

Problema 75

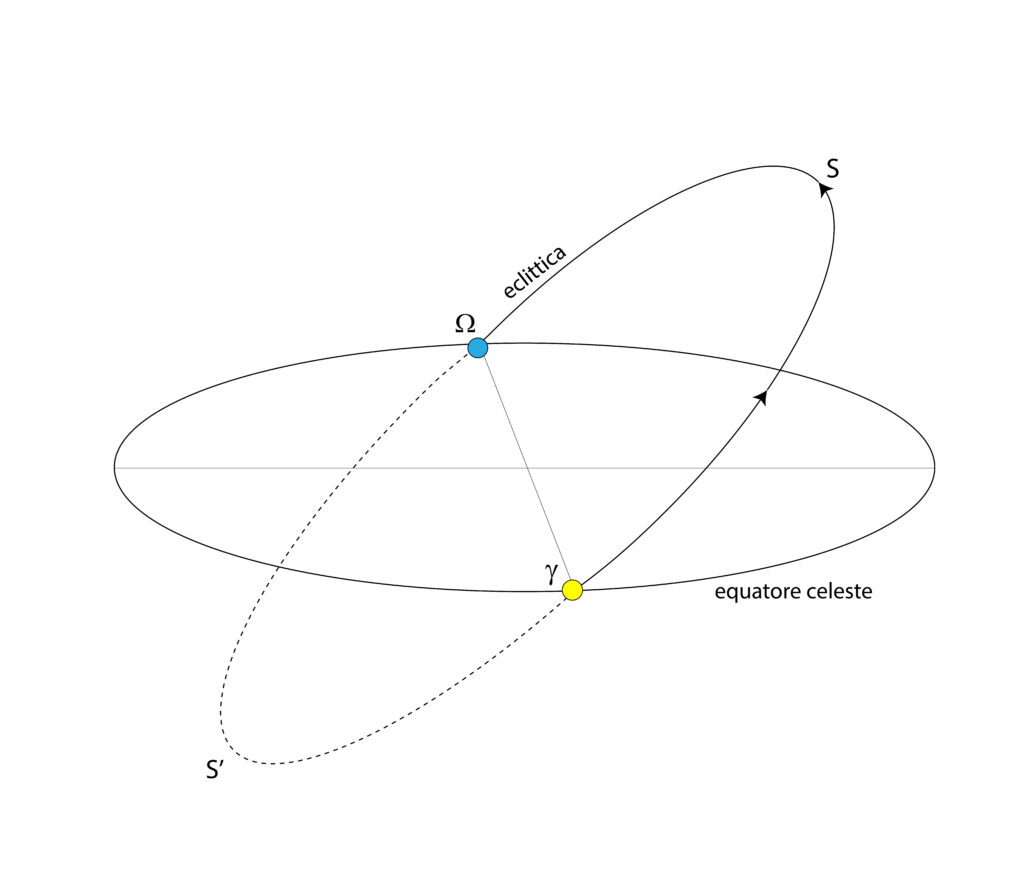
Quali sono i punti della sfera celeste verso i quali si sposta la Terra agli equinozi e ai solstizi? Darne le coordinate equatoriali.

Soluzione. Riferiamoci alla figura seguente, che rappresenta l’equatore celeste e l’eclittica nello spazio all’equinozio di primavera.

La Terra ed il Sole stanno, per definizione, sull’eclittica, inclinata di un angolo di 23,5° sull’equatore celeste, e sono sempre da parti opposte l’una rispetto all’altro (ovvero hanno 12 h di AR di differenza e declinazioni opposte). Di questo passo, ricaviamo la posizione della Terra negli istanti richiesti:

All’equinozio di primavera (Sole: AR=0h, D=0°) la Terra si trova al punto omega (AR=12h, D=0°), e si muove verso il solstizio d’inverno S’;

Al solstizio estivo (Sole: AR=6h, D=23,5°) la Terra si trova in S’ (AR=18h; D=-23,5°) e si dirige verso il punto gamma;

All’equinozio d’autunno (Sole: AR=12h, D=0°) la Terra si trova al punto gamma (AR=0h; D=0°) e si dirige verso il solstizio estivo S;

Al solstizio d’inverno (Sole: AR=18h; D= -23,5°) la Terra si trova in S (AR=6h; D=23,5°) e si muove verso il punto omega.

Problema 76

Quanto dovrebbe durare il giorno su un pianeta delle dimensioni della Terra in rapida rotazione affinché, a causa dell’accelerazione centrifuga, i corpi all’equatore non abbiano alcun peso? Con tale velocità di rotazione, i corpi a latitudine elevata sono ancora attratti dalla Terra?

Soluzione. Si sa che l’accelerazione centrifuga vale in questo caso di moto circolare v²/Rt, con Rt raggio terrestre equatoriale (6380 km). Eguagliandola all’accelerazione g di gravità (annullamento del peso) otteniamo

v²/Rt=g

da cui v= √Rt*g

Il periodo di rotazione richiesto T sarà

T= v/2πRt = 1h 25m.

Alle alte latitudini, la forza peso è approssimativamente sempre costante mentre quella centrifuga dipende dal raggio di rotazione, che decresce come Rt*cosφ (v. problema 71). La risposta alla domanda posta è dunque affermativa.

La Luna

Problema 79

Al primo gennaio di un certo anno cadeva la Luna nuova, alla stessa data dell’anno successivo qual’era l’età della Luna?

Soluzione. Assumiamo per l’anno civile (medio) la durata di 365g e 6h, e per il periodo sinodico della Luna (ovvero il periodo di tempo necessario affinché la Luna ritorni alla stessa fase) 29,5g. Allora in tale periodo la Luna compie 365,25/29,5= 12,4 rivoluzioni. Il primo gennaio dell’anno successivo la Luna avrà quindi un’età di circa 0,4*29,5=12 giorni, e la sua fase sarà intermedia tra il I quarto e il plenilunio.

Problema 84

Qual è il diametro apparente della Terra vista dalla Luna?

Soluzione. La Terra ha un diametro medio di 12.745 km circa, ed è vista dalla Luna alla distanza di circa 385.000 km. Perciò essa sottende un angolo di 12.745/385.000=0,033 rad, pari a circa 2 gradi (4 volte il diametro apparente del Sole visto dalla Terra).

Problema 85

Quali pianeti non possono essere occultati dalla Luna piena?

Soluzione. Sono i pianeti inferiori (Mercurio e Venere). Infatti, la Luna piena si trova dalla parte opposta alla Terra rispetto al Sole (Sole-Terra-Luna) mentre i pianeti inferiori si trovano sempre tra la Terra e il Sole (Sole-Pianeta-Terra).

Problema 83

Se vi trovate sull’equatore lunare, sull’emisfero visibile, ogni quanto tempo vedrete sorgere il Sole? E la Terra?

Problema 86

Come si muovono il Sole e la Terra visti dalla Luna?

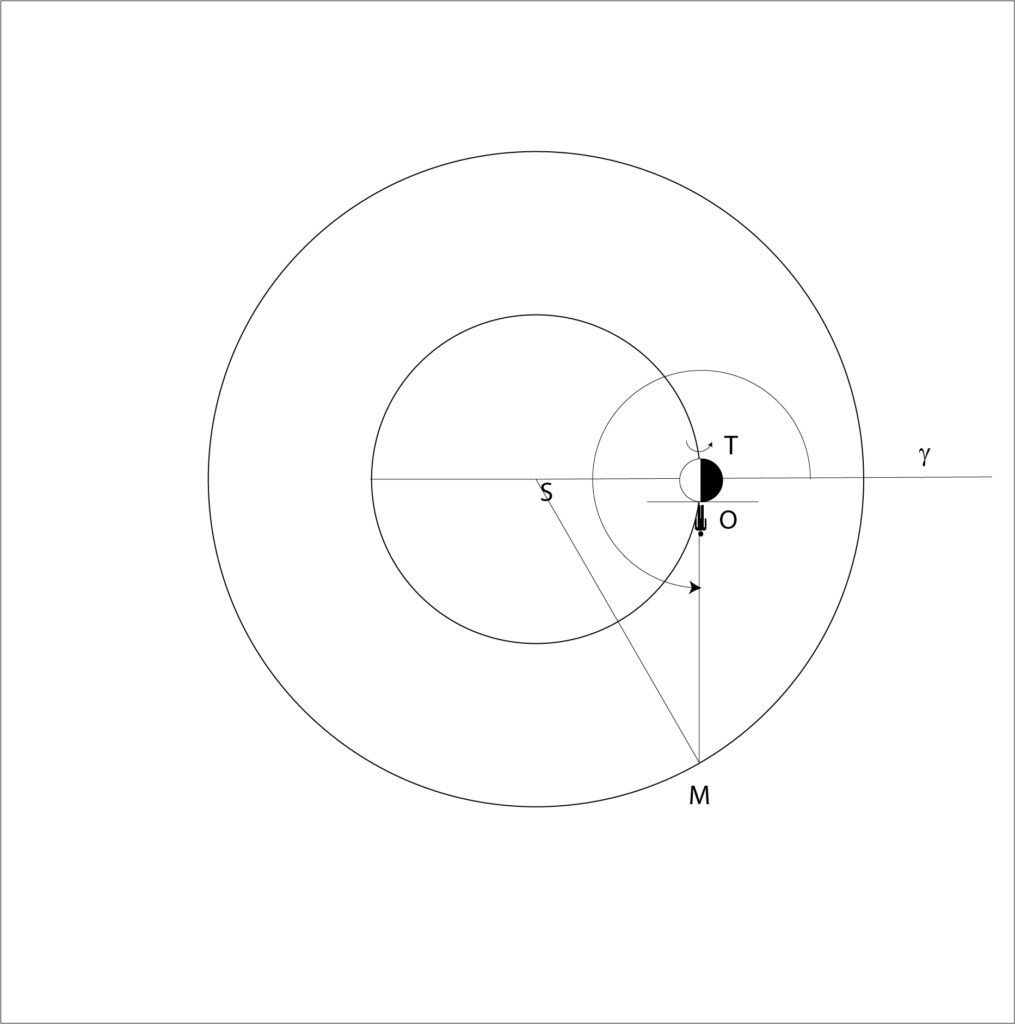
Soluzione. Facciamo riferimento alla figura seguente per i due quesiti sopra.

E’ mostrato il sistema Sole-Luna-Terra, non in scala, visto dal polo nord dell’eclittica; la Luna gira intorno alla Terra in circa 27 giorni, e ruota intorno a sé stessa nello stesso intervallo di tempo. Entrambi i moti avvengono nel senso antiorario. E’ inoltre rappresentato un osservatore A situato sull’equatore lunare, con il suo orizzonte (si noti che l’asse di rotazione lunare è perpendicolare al piano della pagina).

Possiamo anzitutto constatare come le fasi lunari siano effettivamente opposte a quelle terrestri: quando dalla Terra la Luna appare piena, per un osservatore lunare la Terra è nuova, e così via.

Il Sole sorge per l’osservatore lunare nel punto 1, infatti è nella direzione dell’orizzonte e nella stazione precedente (4) era notte. Al punto 2, il Sole si trova all’incirca allo zenit, mentre al punto 3 (dopo due settimane terrestri) avviene il tramonto. A causa della mancanza di atmosfera, i crepuscoli sono istantanei, e si passa immediatamente dalla luce al buio. Al punto 4, è mezzanotte, ed il Sole torna a sorgere ad Est dopo circa una settimana, ad un mese di distanza dall’alba precedente.

Poiché il moto di rivoluzione e quello di rotazione hanno la stessa durata ed entrambi avvengono in senso antiorario, segue che la Terra è stazionaria vista dalla Luna. Infatti, in un periodo di tempo dato, la Terra appare muoversi contro le stelle in senso antiorario a causa della rivoluzione lunare, ed appare contemporaneamente spostarsi di un angolo uguale in senso orario per la rotazione, cosicché i due movimenti si compensano.

Problema 87

La Luna piena è più alta in meridiano d’estate o in inverno?

Soluzione. L’altezza diurna dell’eclittica sull’orizzonte è maggiore d’estate (ricordiamo che il Sole sta sempre sull’eclittica) e minore d’inverno; nell’arco della stessa giornata, inoltre, a grandi altezze eclittiche diurne corrispondono basse altezze notturne, e viceversa. Poiché la Luna piena culmina a mezzanotte, segue che la sua altezza è massima durante il periodo invernale.

Problema 88

A quale latitudine la Luna può passare allo zenit?

Soluzione. Assumiamo che la Luna sia al lunistizio superiore (D=+28,5°) ossia alla massima declinazione del ciclo di 18 anni. Allora (v. problema 20) la corrispondente latitudine di 28.5° è la massima da cui il nostro satellite può transitare allo zenit.

Problema 89

Pressapoco a che ora leva la Luna piena di marzo?

Soluzione. Poiché la Luna piena è in opposizione al Sole, leva al tramonto di quest’ultimo, che intorno all’equinozio di primavera avviene circa alle 18 civili.

Problema 90

Qual è approssimativamente l’ascensione retta della Luna piena all’equinozio di primavera, al solstizio estivo e a quello invernale?

Soluzione. La Luna piena è in opposizione al Sole, dunque a 12h di AR di distanza da questo sull’eclittica (supponiamo, in prima approssimazione, che la Luna orbiti sullo stesso piano dell’orbita terrestre, il che non è del tutto esatto essendo il piano dell’orbita lunare inclinato di 5 gradi). Dunque, essendo nota la posizione del Sole negli istanti richiesti è immediato ricavare quanto richiesto:

equinozio di primavera: AR Sole=0h , AR Luna= 12h:

solstizio estivo: AR Sole: 6h, AR Luna=18h;

solstizio invernale: AR Sole: 18h; AR Luna=6h (c’è un refuso nel testo, che dice 0h).

Problema 92

In dicembre si può vedere la Luna piena al polo Nord? E se la si vede, che altezza massima può avere sull’orizzonte?

Soluzione. Al polo Nord sono visibili (e circumpolari) tutti gli astri, purché la loro declinazione sia maggiore di zero (v. sezione Astronomia sferica). Poiché l’altezza alla culminazione è tanto maggiore quanto maggiore è la declinazione, supponiamo di essere al lunistizio dove δ=+28.5°. Si ha

h = 90°-φ+δ

da cui h=δ=+28.5°.

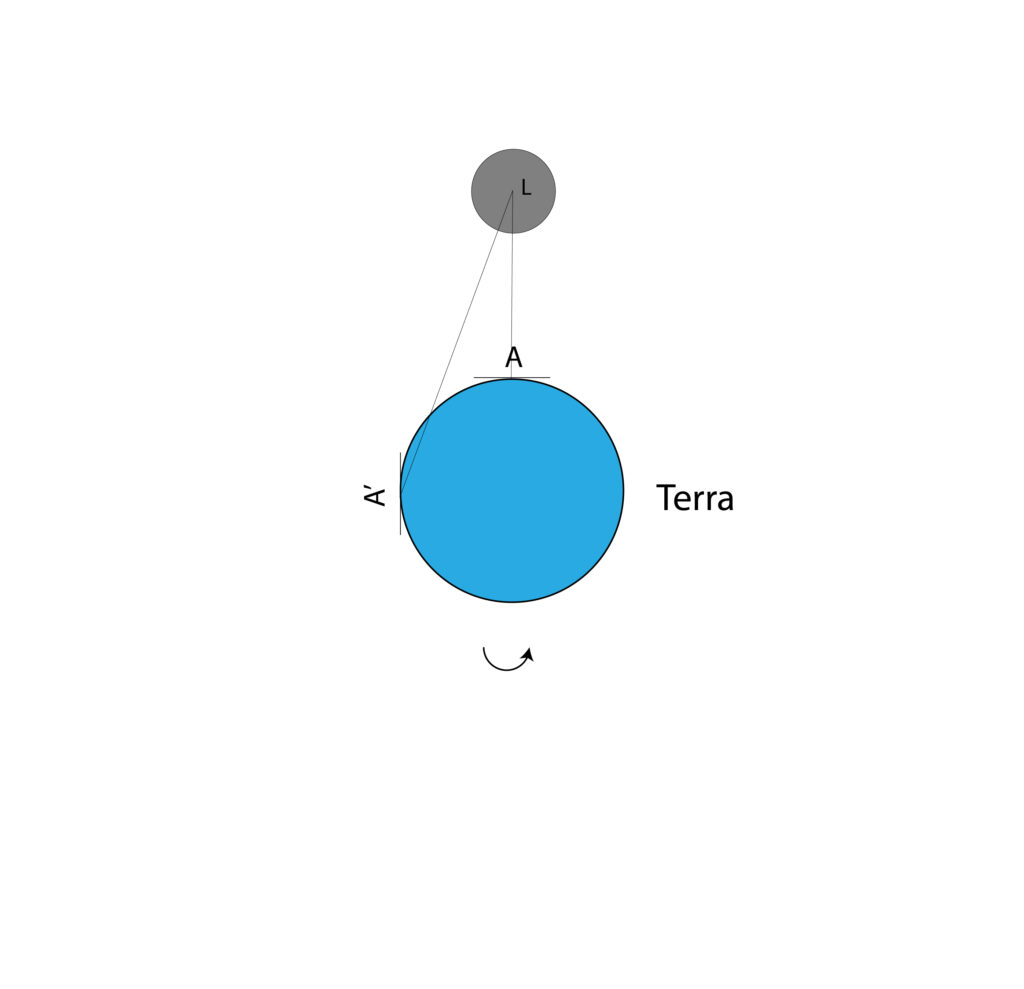
Problema 93

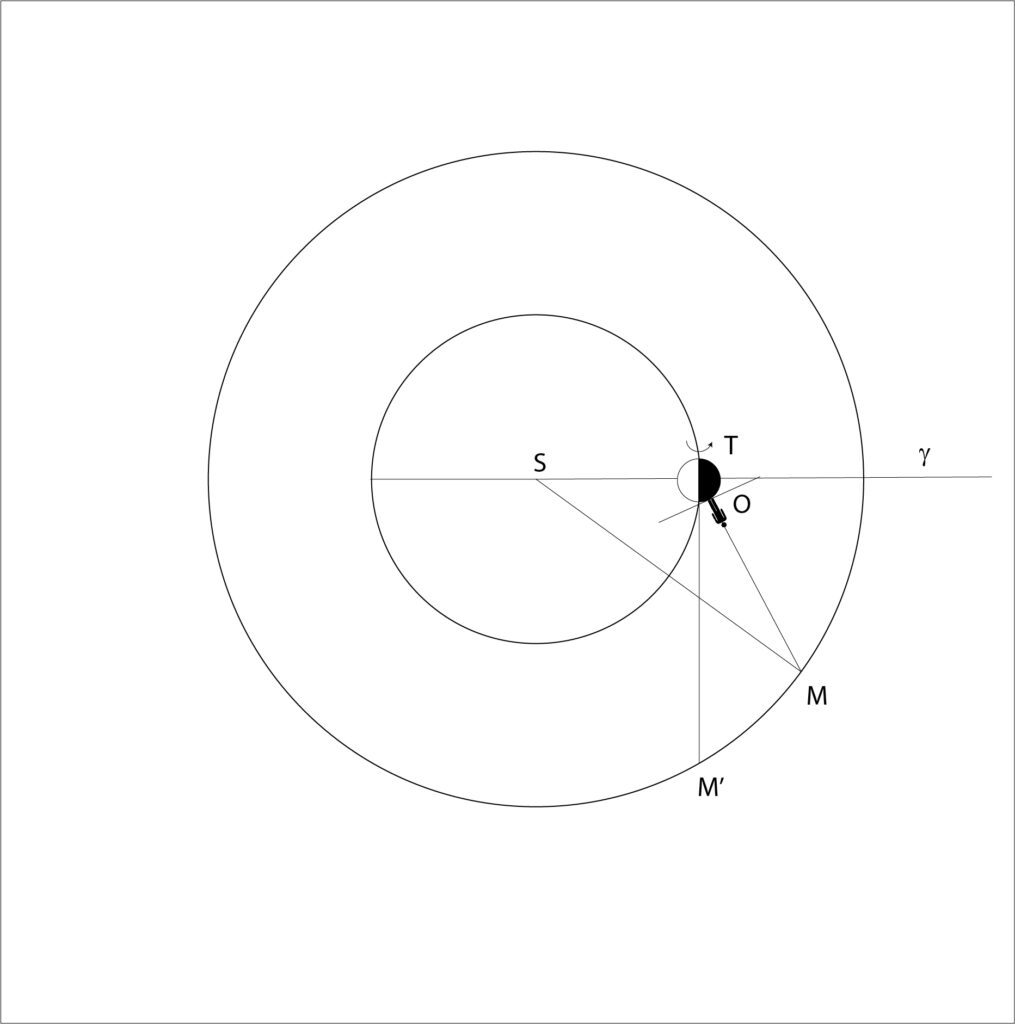
Soluzione. Alla latitudine indicata, al lunistizio superiore (δ=+28.5°) poiché δ=φ come sappiamo la Luna può transitare allo zenit. In figura, è mostrata la Terra, Luna L e un osservatore posto per semplicità sull’equatore, con il suo orizzonte al momento del tramontare della Luna (A’) e del passaggio allo zenit (A). Poiché la distanza AL è sempre minore di A’L, quando la Luna passa al meridiano è sempre leggermente più vicina.

Problema 94

Soluzione. Assumiamo la Luna alla sua massima declinazione, che (vedi testo) è data dalla somma dell’obliquità dell’eclittica e dell’inclinazione dell’orbita: 23° 26′ + 5° 9’= 28° 35′. La minima latitudine a cui la Luna è circumpolare (v. problema 2) è data da

φ = 90° – δ = 61° 25′

Problema 95

Soluzione. La velocità di rivoluzione lunare si ricava facilmente noto il raggio medio dell’orbita e il periodo siderale:

P= 27.33/(2*π*384.400)=3680 km/h=1.02 km/s.

La Luna ha un diametro apparente di circa 0.5°, per cui il suo diametro reale è

384.400*0.5/57.3=3354 km

Dalla costruzione riportata nel testo (fig. 6.1 della terza edizione) e dai dati forniti sappiamo che il diametro del cono d’ombra è circa pari a 2,6 volte il diametro lunare, ossia 8721 km. Per attraversarlo, la Luna impiega

8721 km / 3680 km/h= 2h 22m.

Problema 96

Soluzione. Dal testo, si sa che la distanza d Luna-Terra all’apogeo è a(1+e), con a semiasse maggiore dell’orbita ed e eccentricità. Al perigeo, analogamente, la distanza d’ della Luna dalla Terra è pari a a(1-e), per cui

d/d’= (1+e)/(1-e)

Se moltiplichiamo il primo membro per il diametro D lunare, abbiamo che i termini Dd e Dd’ sono pari al diametro apparente angolare della Luna vista all’apogeo e al perigeo, che sono noti. Quindi

(1+e)/(1-e)= 33’/29.6’=1.11

da cui e=0.054.

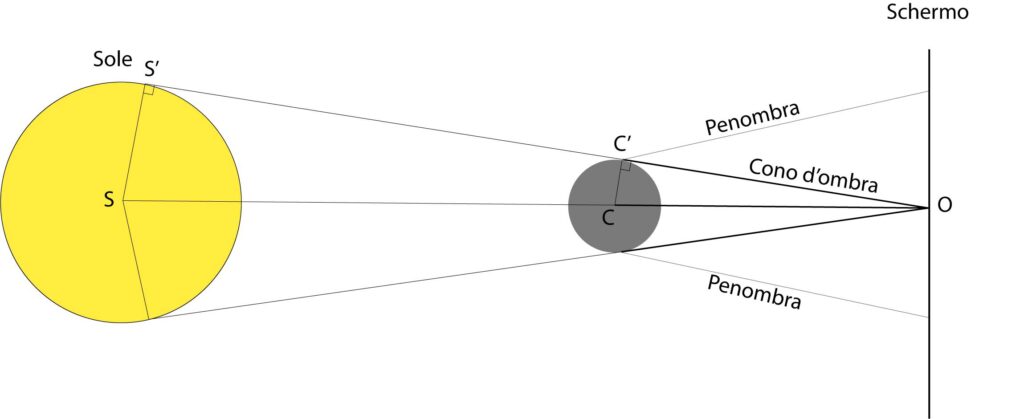
Problema 97

Soluzione. Riferiamoci alla figura sottostante.

Il quesito si risolve osservando che i due triangoli SS’O e CC’O sono entrambi retti e sono simili. Allora si ha

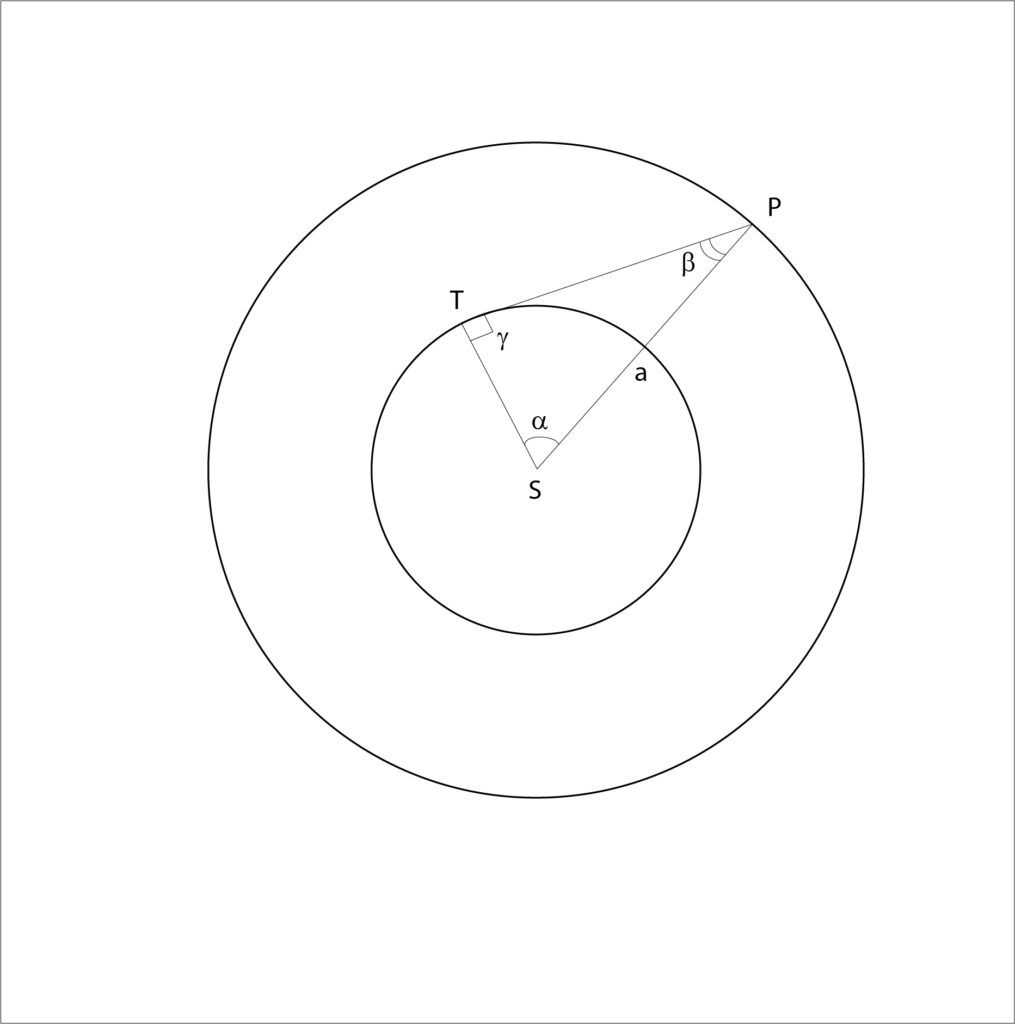
CC’:CO=SS’:SO

ovvero il rapporto tra il raggio della sfera e la sua distanza dallo schermo è pari al raggio SS’ del Sole (ca. 700.000 km) diviso la distanza SO (che è ovviamente l’unità astronomica, 150.000.000 di km).

Affinché la sfera proietti solo penombra, dunque, dev’essere posta ad una distanza di circa 215 volte il suo raggio.

Problema 98

Soluzione. Assumendo per l’anno civile il valore di 365g e 6h e per il periodo siderale quello di 27g 8h, la risposta al quesito è data da

365.25/27.33=13.36

Problema 99

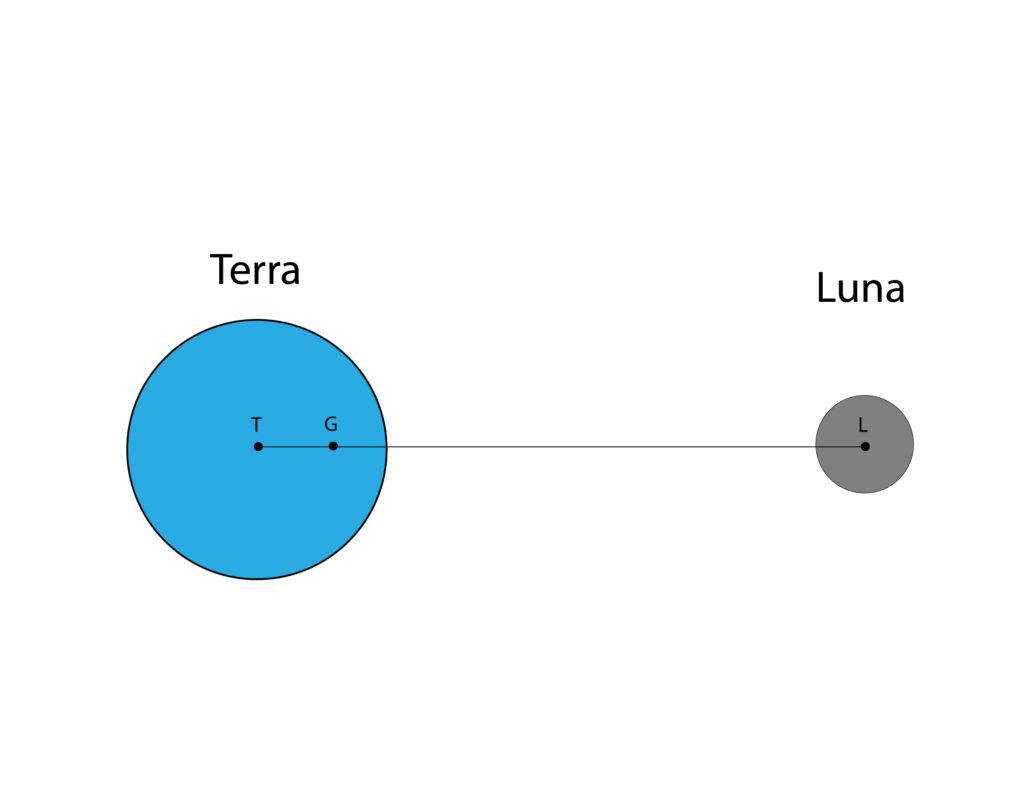
Soluzione. Riferiamoci alla figura seguente, relativa al sistema Terra-Luna, il cui baricentro sia in G.

Dalla definizione di baricentro, dette M ed m rispettivamente la massa della Terra e della Luna

M*TG=m*LG

da cui

TG/LG=m/M=1/81

Del resto

TG+LG=384.400

Mettendo a sistema le due equazioni sopra si trova TG=4687 km. Il baricentro del sistema Terra-Luna è dunque interno alla superficie terrestre.

Problema 100

Soluzione. Il moto apparente della Luna (legato al movimento di rotazione terrestre) da Est verso Ovest non ha alcuna importanza in questo problema. Quello che conta è invece il moto proprio della Luna, che avviene da Ovest verso Est (in senso antiorario per chi lo osserva dal Polo nord dell’eclittica).

Pertanto, il nostro satellite incontra per primo il bordo Ovest del Sole (ovvero quello rivolto ad W).

Problema 102

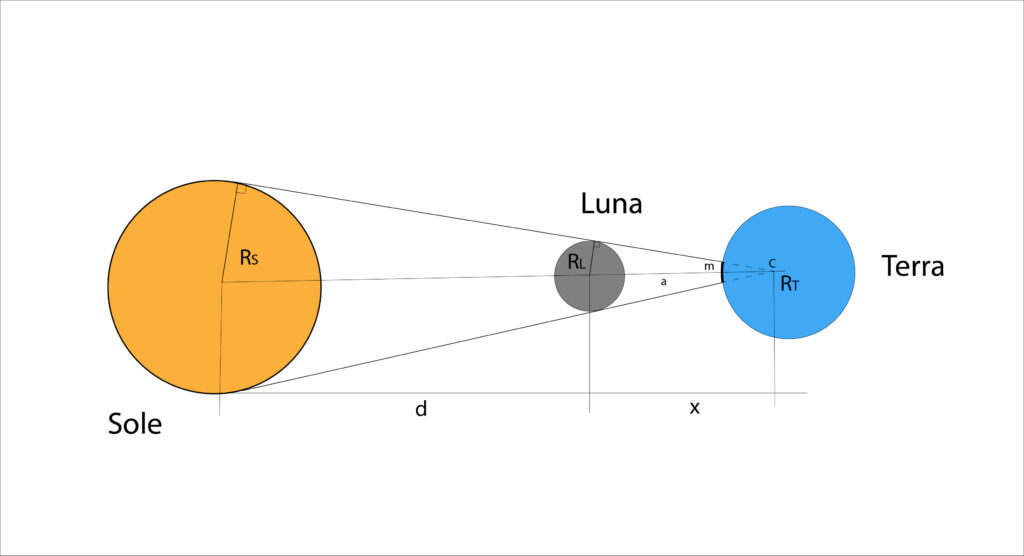
Soluzione. Riferiamoci alla figura sottostante, che mostra il sistema Terra-Sole-Luna durante un’eclisse di Sole. Il disco d’ombra proiettato dalla Luna (che possiamo supporre piatto, data la sua piccola estensione rispetto al raggio terrestre) abbia semidiametro m.

Indicando con d la distanza tra i centi del SoleLuna, pari a 149.6*10⁶ -356*10³= 149.2 *10⁶, dalla similitudine tra triangoli rettangoli abbiamo

R_S:R_L = (d+x):x

da cui x=R_L*d/(R_S-R_L)=374.042 km.

La distanza a tra il centro della Luna e il centro del disco d’ombra è parimenti nota e pari a 356*10³-6378=349.622 km. Si può scrivere l’ulteriore proporzione

R_L:m = x:(x-a)

da cui m=R_L*(x-a)/x=113 km circa.

Problema 103

Soluzione. Si usa la relazione in fondo a pag. 82 della terza edizione (che fa riferimento alla costruzione geometrica di fig. 6.1), la quale dà il valore m cercato, avendo cura di porre il parametro a pari alla distanza minima Terra-Luna ovvero 356.000 km.

Si trova m=4739 km.

Esercitazioni e problemi sui pianeti

Problema 105

Soluzione. I pianeti inferiori (Mercurio e Venere) hanno elongazioni che al massimo raggiungono i 47° nel caso di Venere. Il pianeta è dunque superiore.

Problema 107

Soluzione. Sono naturalmente i pianeti superiori, per i quali l’unica configurazione possibile è Sole-Terra-pianeta, laddove per un transito sul disco solare dovrebbe essere Sole-pianeta-Terra.

Problema 108

Soluzione. I pianeti inferiori sono visibili al mattino ad Est od alla sera ad Ovest; inoltre, i pianeti che sorgono alla sera ad Est sono quelli la cui elongazione è almeno di 180°. La risposta al quesito è dunque i pianeti superiori.

Problema 110

Soluzione. Dai tropici, in cui l’angolo tra l’eclittica e l’orizzonte è sempre particolarmente alto. Infatti (v. sezione Astronomia sferica) poiché la massima declinazione dell’eclittica è +/- 23.5°, i luoghi aventi latitudine compresa tra questi valori sono quelli in cui punti dell’eclittica possono passare allo zenit.

Problema 111

Soluzione. Al perielio marziano (possiamo ricavare i dati dalla tab. a pg. 155 della 3a edizione) si ha che la distanza del pianeta rosso dal Sole è

d=a*(1-e)=1,38 UA

con a semiasse maggiore= 1,52 UA ed e eccentricità=0,093. Essendo l’orbita terrestre pressoché circolare, la distanza Terra-Marte sarà pari a 1,38-1=0,38 UA=56,8 milioni di km. La distanza Terra-Luna è. in media, di 384.000 km, per cui l’angolo sotto cui questa distanza appare da Marte è (1 rad=57,3 gradi):

384.000/56,8*10⁶ *57.3= 23′.

Problema 112

Qual è il diametro apparente del Sole visto da Mercurio quando il pianeta è all’afelio ed al perielio (a=57,8 milioni di km; e=0,2)?

Soluzione. Il diametro del Sole è pari a circa 1,4*106 km. All’afelio, la distanza Mercurio-Sole è

dA=a(1+e)=6,94*107 km

e al perielio

dP=a(1-e)=4,63*107 km

Il diametro angolare del Sole visto da Mercurio è dunque, all’afelio:

d’=(1,4*10⁶/6,94*10⁷) *57,3=1°9′

e al perielio

d”= (1,4*10⁶/4,63*10⁷)*57,3=1*43′.

Poiché dalla Terra il Sole sottende un angolo di circa mezzo grado, da Mercurio la nostra stella appare dalle 2 alle 3 volte più grande.

Problema 113

Se da Saturno si osserva il passaggio della Terra di fronte al disco del Sole, con quale diametro apparente si vedrebbe il dischetto nero della Terra, e a quale distanza angolare apparirebbe il dischetto della Luna se fosse in quadratura?

Soluzione. La distanza media di Saturno dal Sole è a=9,53 UA. Quindi la distanza media Saturno-Terra è 8,53 UA=1,27*10⁹ km. Allora la Terra in transito avrebbe diametro apparente

(2*6350/1,27*10⁹) *206.265=2″

La Luna in quadratura apparirebbe alla massima distanza angolare dalla Terra, data da

(384.000/1,27*10⁹) *206.265= 60″=1′.

Problema 114

Qual è il diametro apparente di Plutone visto dal Sole e quanto più debole apparirebbe rispetto a come lo vediamo dalla Terra?

Soluzione. Plutone dista, in media, 39 UA. Siccome la distanza Terra-Sole è pari ad 1 UA, il diametro apparente del Sole da Plutone è 39 volte minore quello visto dalla Terra, pari a mezzo grado:

30/39*60=46″.

Il flusso luminoso proveniente dal pianeta diminuisce con il quadrato della distanza, ed esso apparirebbe perciò (39)² = 1521 volte più debole.

Problema 116

La distanza Terra-Sole varia da 147 a 152 milioni di km. Trovare l’eccentricità dell’orbita terrestre.

Soluzione. Detto a il semiasse maggiore dell’orbita, si ha come già visto per la distanza Terra-Sole all’afelio

dA= a(1+e)= 152.000.000

ed al perielio

dP= a(1-e)=147.000.000

Dividendo membro a membro e risolvendo per l’eccentricità, si trova e=0,016.

Problema 117

Sapendo che il Sole visto dalla Terra sottende un angolo di circa 32′, quanti primi d’arco sottende visto dagli altri pianeti?

Soluzione. Si veda il problema 114.

Problema 118

Quali sono le massime elongazioni degli altri pianeti visti da Saturno?

Soluzione. Riferiamoci alla figura seguente, che mostra l’orbita della Terra T e quella di Saturno P, supposte per semplicità circolari. La Terra, vista da Saturno, sia in quadratura, a cui corrisponde la massima distanza angolare (β) dal Sole S vista da Saturno. La distanza di Saturno dal Sole, espressa in Unità Astronomiche, sia a.

Poiché per definizione di massima elongazione l’angolo γ è retto, si ha

sin β= 1/a=1/9,53=0,105

da cui

β=arcsin (0,105) ≈ 6°.

I casi degli altri pianeti (quelli interni rispetto a Saturno, cioè da Marte a Mercurio) si trattano in modo analogo.

Problema 120

Lo sciame delle Perseidi ha una distanza perielica q=0,94 UA e una eccentricità di 0.96. Trovare il periodo della massima attività.

Soluzione. Il periodo del massimo coincide approssimativamente con il perielio della cometa, per il quale si ha

q=a(1-e)

da cui a=23,5 UA.

Scriviamo ora la terza legge di Keplero per la Terra

P²_T=ka_T³

e per la cometa

P²_C=ka_C³

Esprimendo il periodo in anni, e il semiasse maggiore in UA, dalla prima relazione troviamo k=1, e dalla seconda

Pc= √a_C³= 114 anni.

Problema 122

In un disegno nel quale il semiasse maggiore dell’orbita terrestre è 1 metro, quanto è lungo l’asse minore?

Soluzione. L’eccentricità dell’orbita terrestre è e=0,017 ed è uguale per definizione a c/a (v. capitolo del libro sulle proprietà dell’ellisse), da cui c=ea=1,7 cm. Dal teorema di Pitagora, l’asse minore b sarà pari a

b=√(a²-c²)=0,9998 m= 99,98 cm.

Problema 124

Sapendo che il semiasse maggiore dell’orbita terrestre è 146,6 milioni di km (e=0,017) qual è la variazione massima in km della distanza Terra-Sole? E quant’è la distanza del Sole dal centro dell’ellisse?

Soluzione. All’afelio, come già visto in altri esercizi, distanza Sole-Terra è

dA= a(1+e)

e al perielio

dP=a(1-e)

Quindi

dA-dP= 2ae=5,1*10⁶ km.

La distanza del Sole dal centro dell’ellisse è data da

c=ea=2,5*10⁶ km

Problemi 126-127-128

Qual è la parallasse del Sole vista da Giove? […]

Soluzione. Riportiamo qui solo il testo e la soluzione del problema 126, visto che gli altri due sono del tutto simili. Per definizione, la parallasse di Giove è l’angolo sotteso dal raggio del pianeta alla distanza del Sole, per cui esprimendo tutto in km e convertendo in secondi d’arco

R_giove/d_giove= (69.911/777,9*10⁶)*206.265= 19″.

Problema 130

All’equinozio la longitudine geocentrica del Sole sia 180°, in quel giorno Marte passi in meridiano alle 18h. Trovare la distanza Terra-Marte (distanza Marte-Sole 1,52 UA) e la longitudine geocentrica di quest’ultimo.

Soluzione. Riferiamoci al disegno seguente, che mostra (non in scala) le orbite della Terra T, e di Marte M, supposte circolari e centrate sul Sole S. E’ mostrato un osservatore O con il suo orizzonte, supposto per semplicità equatoriale; si noti che la figura mostra i movimenti dei due pianeti come osservati dal polo Nord dell’eclittica (la Terra ruota in senso antiorario).

Dal teorema di Pitagora, applicato al triangolo TSM, si ha

TM=√(SM²– ST²)= √(1,54²-1²)=1,14 UA.

La longitudine geocentrica di Marte è rappresentata dall’angolo γTM, pari a 270 gradi.

Problema 131

Risolvere lo stesso problema supponendo che Marte passi al meridiano alle 20h 35m (per risolvere il problema occorre la trigonometria).

Soluzione. Si faccia riferimento alla figura seguente.

Rispetto al caso precedente, in cui era in M’, Marte si è spostato in M. Ora Marte culmina 20,35h-18h=2,35h ore più tardi, che ricordando l’equivalenza 1h=15° per la rotazione terrestre equivalgono a circa 37°. Dunque l’angolo STM (che nel problema precedente era retto) ora è pari a 90°+37*=127°. Applicando il teorema di Carnot al triangolo STM

SM²=ST²+TM²-2ST*TM*cos (STM)

da cui indicando con x la distanza Terra-Marte, e supponendo sempre pari a 1,52 UA la distanza Marte-Sole (orbita circolare)

(1,52)²=1²+x²+1.2x

riordinando

x²+1,2x-1,31=0

Risolvendo l’equazione di II grado si trova x=0,70 UA.

La longitudine geocentrica di Marte risulta naturalmente pari a 270°+37°=307°.

Problema 134

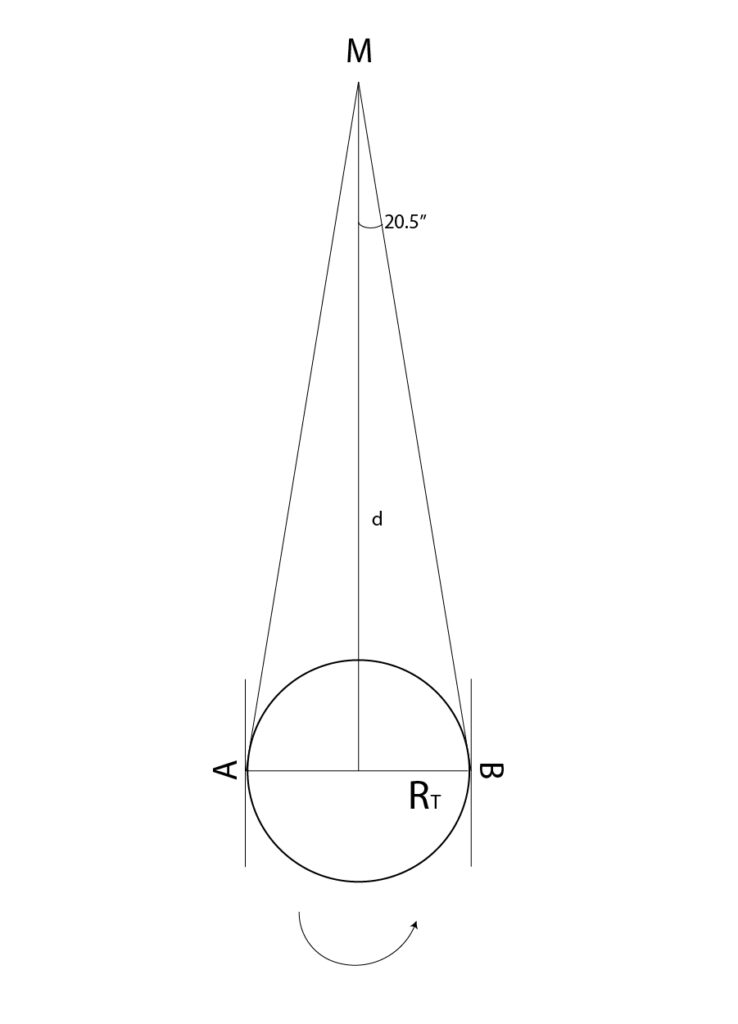
Marte, che un giorno si trovava sull’equatore celeste, fu osservato da due località sull’equatore terrestre in modo che dalla prima località lo si vedeva all’orizzonte Est, dall’altra all’orizzonte Ovest. I due osservatori notarono che la posizione di Marte sulla sfera celeste differiva di 41″. A che distanza si trovava Marte e in quale posizione rispetto alla Terra?

Soluzione. I due osservatori misurano, in sostanza, la parallasse di Marte, e si trovano l’uno agli antipodi dell’altro (ricordiamo che la differenza tra le longitudini è uguale a quella tra gli angoli orari osservati, che in questo caso è pari a 12h).

La figura schematizza la situazione, mostrando i due osservatori equatoriali A e B con i loro orizzonti, osservati dal polo Nord eclittico. Per B Marte sorge mentre per A tramonta.

Per definizione di parallasse (con Rt raggio terrestre equatoriale=6378 km, e d distanza cercata)

(Rt/d)*206.265=20.5″ da cui d=64*10⁶ km.

La configurazione geometrica mostrata, con Marte allineato alla Terra rispetto al Sole (qui non mostrato, in basso nel disegno) corrisponde al pianeta all’opposizione. Se così non fosse e Marte si trovasse più ad Est o ad Ovest, i due osservatori non potrebbero vederlo contemporaneamente (infatti, è sempre sotto l’orizzonte di uno dei due, come è facile constatare). Il caso di congiunzione con il Sole si esclude in quanto il pianeta è inosservabile in quei giorni.

Problema 135

Il periodo siderale di Saturno è 29,4 anni. Il pianeta è stato in opposizione il 21 aprile 1983; quando cadrà pressappoco la prossima congiunzione?

Soluzione. Poiché il pianeta è molto lento rispetto alla Terra nel suo moto di rivoluzione, possiamo supporlo immobile per periodi di tempo relativamente brevi. Poiché all’opposizione si ha la configurazione Sole-Terra-Pianeta, mentre alla congiunzione Sole-Pianeta-Terra, per passare dall’una all’altra la Terra deve spostarsi dall’altra parte della propria orbita, impiegando circa 6 mesi. La congiunzione del pianeta con il Sole avverrà dunque verso la fine di ottobre del 1983.

Problema 136

Se il raggio vettore di un asteroide in 5 mesi descrive 1/10 dell’area totale racchiusa dalla sua orbita, quant’è il periodo dell’asteroide?

Soluzione. Per la seconda legge di Keplero, l’asteroide percorre aree uguale in tempi uguali, ed impiegherà quindi circa 5*10=50 mesi per completare l’orbita.

Problema 137

Se la nube di Oort si trova a 100.000 UA dal Sole, quant’è il periodo di una cometa proveniente da tale regione?

Soluzione. Dalla terza legge di Keplero, scrivendo il periodo P in anni e il semiasse maggiore in UA, abbiamo

P²=a³

da cui P=√a³= 10⁷ anni.

Problema 139

Una opposizione di Marte è avvenuta il 31 marzo 1982, essendo il suo periodo siderale pari a 687 giorni, in quale anno e quale mese cadrà la prossima opposizione?

Soluzione. Il problema richiede il periodo sinodico di Marte. Si suppongono le orbite circolari, e si applica l’equazione del moto sinodico

P=SA/(S-A)

con P periodo siderale ed S periodo sinodico del pianeta in anni, ed A anno siderale terrestre (quindi pari ad 1). Si ha

1,88=S/(S-1)

da cui S=2,136 anni= 2 anni 1 mese e 19 giorni. Poiché il 1982 non era bisestile, la prossima opposizione di Marte si sarebbe avuta secondo il calcolo (errato di più di una settimana perché non considera l’eccentricità dell’orbita marziana) il 19 maggio 1984.

Problema 140

Qual è il periodo siderale di un pianeta il cui periodo sinodico è 1,09 anni? Che pianeta è?

Soluzione. Supponiamo che il pianeta sia interno. Con gli stessi simboli dell’esercizio precedente, scriviamo

P=S/(S+1)

da cui P=0,52 anni, che non corrisponde al periodo siderale né di Venere né di Mercurio. Allora, facendo l’ipotesi di pianeta esterno

P=S/(S-1)

da cui P=12 anni. Il pianeta cercato è dunque Jupiter.

Problema 141

Quale periodo siderale avrebbe un pianeta se quel periodo fosse uguale al sinodico?

Soluzione. Supponiamo si tratti di un pianeta interno, per il quale scriviamo

P=S=S/(S+1)

da cui S=0 che è impossibile.

Nell’ipotesi di pianeta esterno, abbiamo invece

P=S=S/(S-1)

da cui

S²-2S=0

Scartando la radice nulla di questa equazione, che non ha significato fisico, si ha S=2 anni.

Problema 143

Giove in una certa epoca ha mostrato un diametro equatoriale di 37″.42 e uno polare di 35″,02. Trovare lo schiacciamento del pianeta.

Soluzione. Detti a e b i due raggi equatoriale e polare rispettivamente, si usa per lo schiacciamento s la relazione

s=(a-b)/a=1-b/a=0,065.

Si noti che lo schiacciamento così definito è diverso dall’eccentricità di un’orbita.

Problema 145

Un pianeta ha periodo sinodico di 584 giorni, qual è la sua distanza dal Sole?

Soluzione. Supponendo che il pianeta sia esterno, applichiamo la relazione del moto sinodico

P=S/(S-1)

dove i simboli hanno il significato già visto. Sostituendo per S=584 g=1,60 anni si trova P=2,67 anni, che non corrisponde al periodo siderale di nessun pianeta del Sistema Solare.

Nell’ipotesi di pianeta interno invece

P=S/(S+1)

da cui P=0,61 anni, e dalla terza legge di Keplero a= ∛P²=0,72 UA, che corrisponde al semiasse maggiore dell’orbita venusiana.

Problema 147

Determinare il periodo sinodico di Callisto visto da Giove, sapendo che il suo periodo siderale è di 16,69 giorni e che il periodo siderale di Giove è di 11,86 anni.

Soluzione. Il sistema Callisto-Giove si può assimilare al sistema Terra-Luna, per il quale è spiegato nel libro il calcolo del periodo sinodico lunare (S) a partire dal mese siderale M e dall’anno siderale A. La relazione è

S=MA/(A-M)

In questo caso, Giove prende il posto della Terra (A=11,86 anni) e M è il periodo siderale di Callisto, pari a 16,69 giorni. Facendo i calcoli, si trova S=16,75g= 16g 18h (il testo dice 16hg 15h, ma è probabilmente un refuso).

Problema 151

Se esistesse un decimo pianeta ed obbedisse alla legge di Bode, a che distanza si troverebbe dal Sole e che periodo avrebbe?

Soluzione. La legge di Titius-Bode si scrive (a=semiasse maggiore dell’orbita in UA)

a=0,4+0,3*2ⁿ

dove n vale -∞ per Mercurio, 0 per Venere, 1 per la Terra…eccetera, fino ad arrivare a Plutone che avrebbe n=8 contando anche l’asteroide Cerere, la cui orbita, compresa tra Marte e Giove, è calcolata con sufficiente accuratezza dalla legge. Per un ipotetico decimo pianeta, con n=9, si avrebbe

a= 0,4+0.3*2⁹= 154 UA

e dalla terza legge di Keplero

P=√a³= 1911 anni.

Problema 152

Gli anelli di Saturno hanno rispettivamente come minimo e massimo diametro circa 144.000 e 275.000 km. Quanto maggiore è il periodo di rivoluzione della parte esterna dell’anello rispetto a quella interna?

Soluzione. Gli anelli di Saturno sono formati da corpuscoli rocciosi che si possono considerare come satelliti in orbita intorno al pianeta. Allora l’anello esterno avrà (per la terza legge di Keplero) un periodo orbitale P1 più lungo di quello interno P2; ed è possibile scrivere

P1²=ka1³

e

P2²=ka2³

da cui rapportando membro a membro

P1/P2=√(a1/a2)³=2,6.

Problema 152

A che distanza deve trovarsi un satellite artificiale di Marte dal centro del pianeta, affinché sia sincrono con la sua rotazione?

Soluzione. E’ possibile applicare anche al satellite artificiale la terza legge di Keplero, prima però si deve ricavare la costante k (che non è più unitaria come quando ci si riferisce alla rivoluzione dei pianeti intorno al Sole). Per farlo, è possibile utilizzare uno dei due satelliti naturali del pianeta, Phobos e Deimos, dei quali sono noti i parametri orbitali. Ad esempio, per Phobos, P=0,31g=7,4h e a=23.459 km, da cui

k=P²/a³=7,3*10^-11 h²/km³

Applicando ora la terza legge al satellite artificiale (possiamo assumere il periodo di rotazione di Marte pari a 24h)

a=∛(P²/k)= 20.000 km circa.

Problema 157

Giove è all’opposizione. Marte, visto dalla Terra, dista 10° da Giove; Marte dista dalla Terra 0,52 UA. A quale distanza si trova approssimativamente Marte da Giove?

Soluzione. Riferiamoci alla figura seguente, ovviamente non in scala, che mostra la configurazione planetaria descritta nel testo dell’esercizio. La distanza all’opposizione di Giove è pari a 4,20 UA. Si può ricavare o direttamente dalle tabelle oppure osservando che l’orbita di Giove è pressoché circolare, ed il suo semiasse maggiore è 5,20 UA da cui sottraendo la distanza Terra-Sole pari ad 1 UA si arriva al valore cercato.

Applicando il teorema del coseno al triangolo TMG

MG²=TM²+TG²-2*TM*TG*cos(10°)

si trova MG=3,69 UA=552*10⁶ km.

Problema 160

Due osservatori posti a 160 km l’uno dall’altro in linea d’aria su un meridiano terrestre notano contemporaneamente la traccia di una meteora. Quello a N la vede in meridiano verso S ad un’altezza di 45°, l’altro la vede alla stessa altezza ma verso N. Quanto è alta dalla superficie della Terra la traccia della meteora in questione?

Soluzione. Il problema è notevolmente semplificato dal fatto che i due osservatori sono sullo stesso meridiano, sono vicini (sicché è possibile trascurare la curvatura terrestre senza errore sensibile) e vedono entrambi la meteora M in meridiano. Dalla costruzione sotto, essendo i due triangoli rettangoli isosceli, segue immediatamente che l’altezza h della meteora è uguale alla metà del segmento AB, ossia 80 km.